Предмет: Алгебра,
автор: zhamashzhannur
плиз сделайте пожалуйста побыстрее
Приложения:
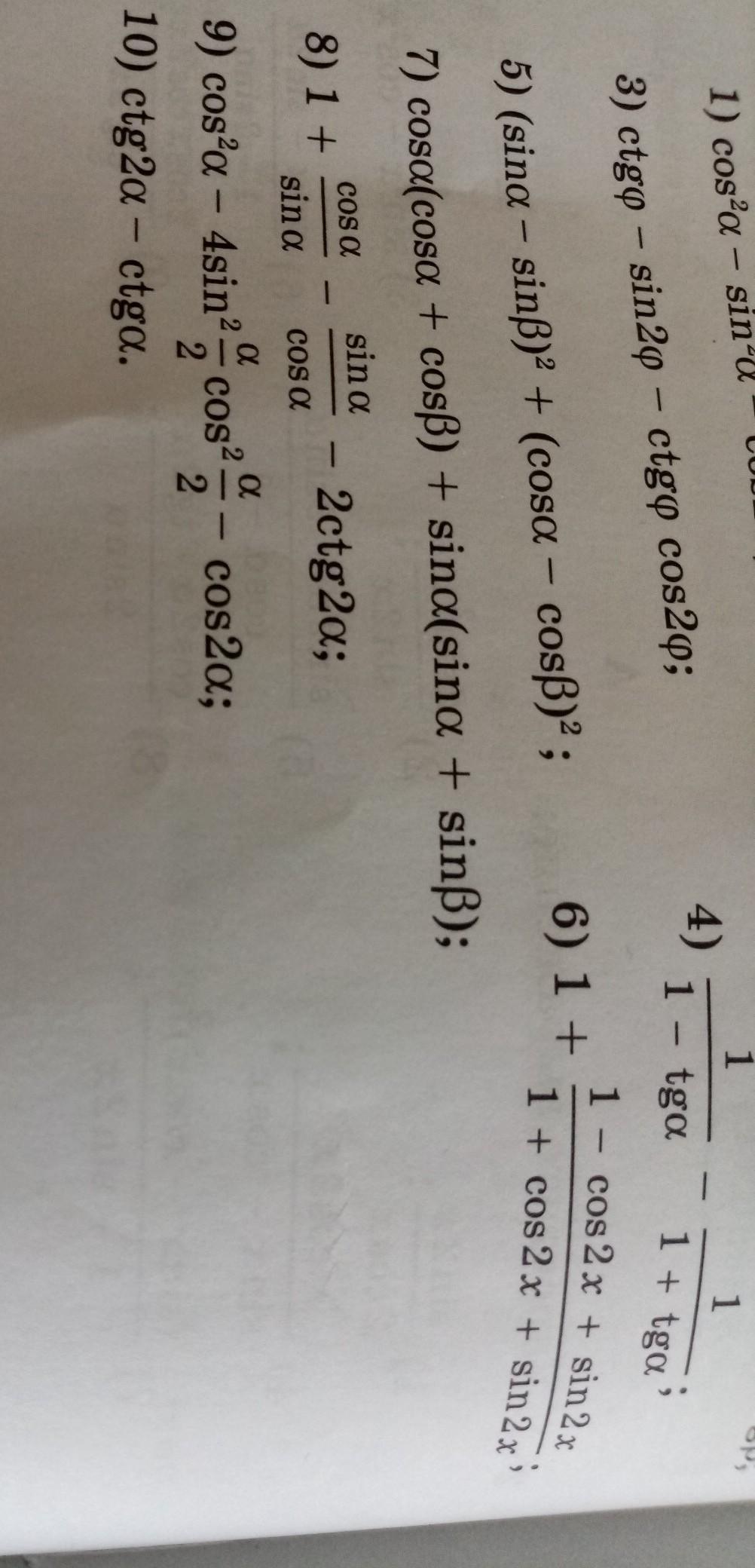
Ответы
Автор ответа:
1
Ответ:
3
4
5
6
7
8
9
10
Похожие вопросы
Предмет: Русский язык,
автор: ksuhaSharova97
Предмет: Английский язык,
автор: alinochka1519
Предмет: Русский язык,
автор: школа137
Предмет: Беларуская мова,
автор: 345153
Предмет: Математика,
автор: sofyaagafonova