Предмет: Математика,
автор: ogog6625
ПОМОГИТЕ СРОЧНО ОЧЕНЬ!!!!!! решите производности.ПРОШУ
Приложения:
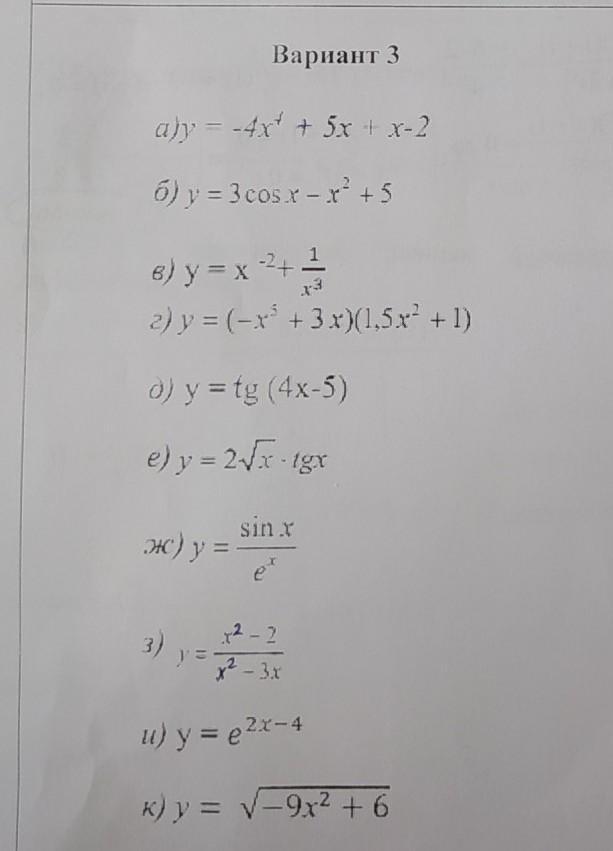
Ответы
Автор ответа:
2
Ответ:
а
б
в
г
д
е
ж
з
и
л
Похожие вопросы
Предмет: Русский язык,
автор: помидор2
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: ZANdi
Предмет: Математика,
автор: barnonur72
Предмет: Математика,
автор: Наза1111