Предмет: Алгебра,
автор: maskskinsite
Интеграл. Помогите решить.
Приложения:
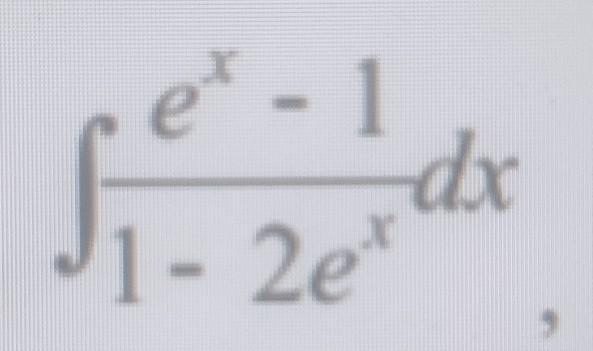
Ответы
Автор ответа:
1
maskskinsite:
куда делся -1
последняя строчка
И почему от -ln(e^x) получился -1
-x же вроде
Вы тут ?
MIRISLAVA ?
Помогите пожалуйста
при обратной замене ln(e^x)= x у Вас -1
вообще решение правильное ?
что- то мне кажется что ответ подогнан под правидьный
Похожие вопросы
Предмет: Русский язык,
автор: xabibulinairina
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: Masha12200516
Предмет: Литература,
автор: lara1112