Question

Помогите, пожалуйста с задачей!!!
Точка D равноудалена от вершин прямоугольного треугольника ABC(угол ACB=90°). Найдите угол между плоскостями ABC и ACD, если AC=BC=2см, а точка D удалена от плоскости ABC на √3 см.

Answer 1

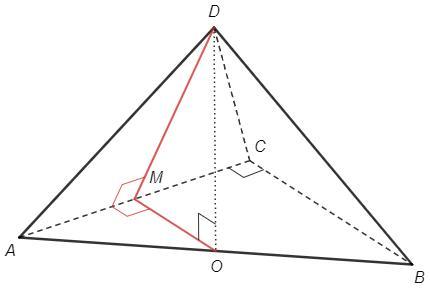
Пирамида, боковые грани равны - вершина проецируется в центр описанной окружности основания.

Центр описанной окружности прямоугольного треугольника - середина гипотенузы (O).

DO⊥(ABC), DO=√3

MO - средняя линия, MO=BC/2=1, MO||BC => MO⊥AC

DM⊥AC (по теореме о трех перпендикулярах)

∠DMO - линейный угол двугранного угла DACB (угол между перпендикулярами к линии пересечения плоскостей)

tg(DMO) =DO/MO =√3 => ∠DMO=60°