Предмет: Геометрия,
автор: ubeysyabeach
помогите пожалуйста, 7 класс геометрия
Приложения:

Ответы
Автор ответа:
2
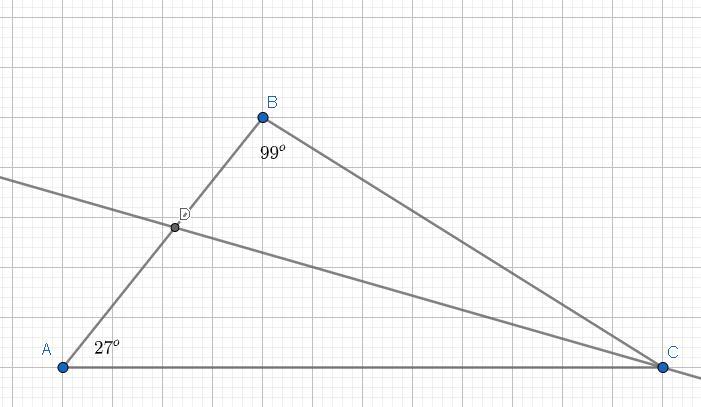
1. Для начала найдём все углы треугольника ΔABC.
<A = 27°; <B = 99° ⇒ <C = 180-(99+27) = 54°.
Так как биссектриса CD — делит угол <C на 2 равные части, то: <DCA = 54/2 = 27°.
Тоесть: <DAC == <DCA ⇒ DA == DC, что и означает, что треугольник ΔADC — равнобёдренный, так как боковые стороны равны.
2.
Угол — противоположный стороне DB — это <BCD, который в треугольнике ΔDBC — считается самым маленьким углом — 27°.
А сторона, противолежащая самому маленькому углу — считается самой маленькой стороной в определённом треугольнике.
В треугольнике ΔADC — опять же, самый маленький угол — <A (27°), а противолежащая ему сторона — DC, которая самая маленькая в треугольнике ΔADC.
И так как углы совпадают, то стороны равны, тоесть BD == CD.
Приложения:
Автор ответа:
2
Доказательство а)
1) 180° - (27°+99°)=54° - угол С
2) 54°/2=27° - углы А и С по отдельности, значит треугольник АDC - равнобедренный
1) 180° - (27°+99°)=54° - угол С
2) 54°/2=27° - углы А и С по отдельности, значит треугольник АDC - равнобедренный
Похожие вопросы
Предмет: Английский язык,
автор: koryakinanatul
Предмет: Русский язык,
автор: окси6
Предмет: Русский язык,
автор: светка30
Предмет: Русский язык,
автор: hibito2