Question

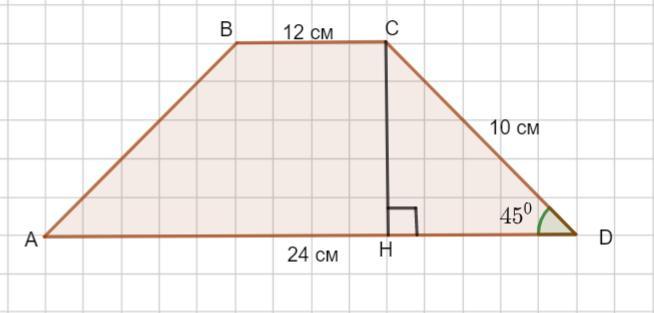
Подскажите основания трапеции bc и ad равны 12 и 24, боковая сторона cd= 10 см образует с большим основанием 45 градусов. найти площадь трапеции.​

Answer 1

Ответ:

Площадь трапеции равна 90√2 см².

Объяснение:

Пусть дана трапеция ABCD  . Основания трапеции ВС= 12 см,

AD= 24 см , боковая сторона CD= 10 см , ∠D= 45°.

Проведем высоту трапеции  СН .

Рассмотрим Δ CHD- прямоугольный.   ∠D= 45°.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе .

$sin D= \dfrac{CH}{CD} ;\\\\sin45^{0} =\dfrac{CH}{10} ;\\\\\dfrac{\sqrt{2} }{2} =\dfrac{CH}{10} ;\\\\CH=\dfrac{10\sqrt{2} }{2} =5\sqrt{2}$

Значит, высота трапеции равна 5√2 см.

Площадь трапеции найдем как произведение полусуммы оснований на высоту трапеции.

$S= \dfrac{BC+AD}{2} \cdot CH;\\\\S= \dfrac{12+24}{2} \cdot 5\sqrt{2} =\dfrac{36}{2} \cdot 5\sqrt{2}=18\cdot 5\sqrt{2}=90\sqrt{2}$

Тогда площадь трапеции равна 90√2 см².