Question

сопоставить фигуру с формулой площади, срочно.​

Answer 1

Объяснение, ответ:

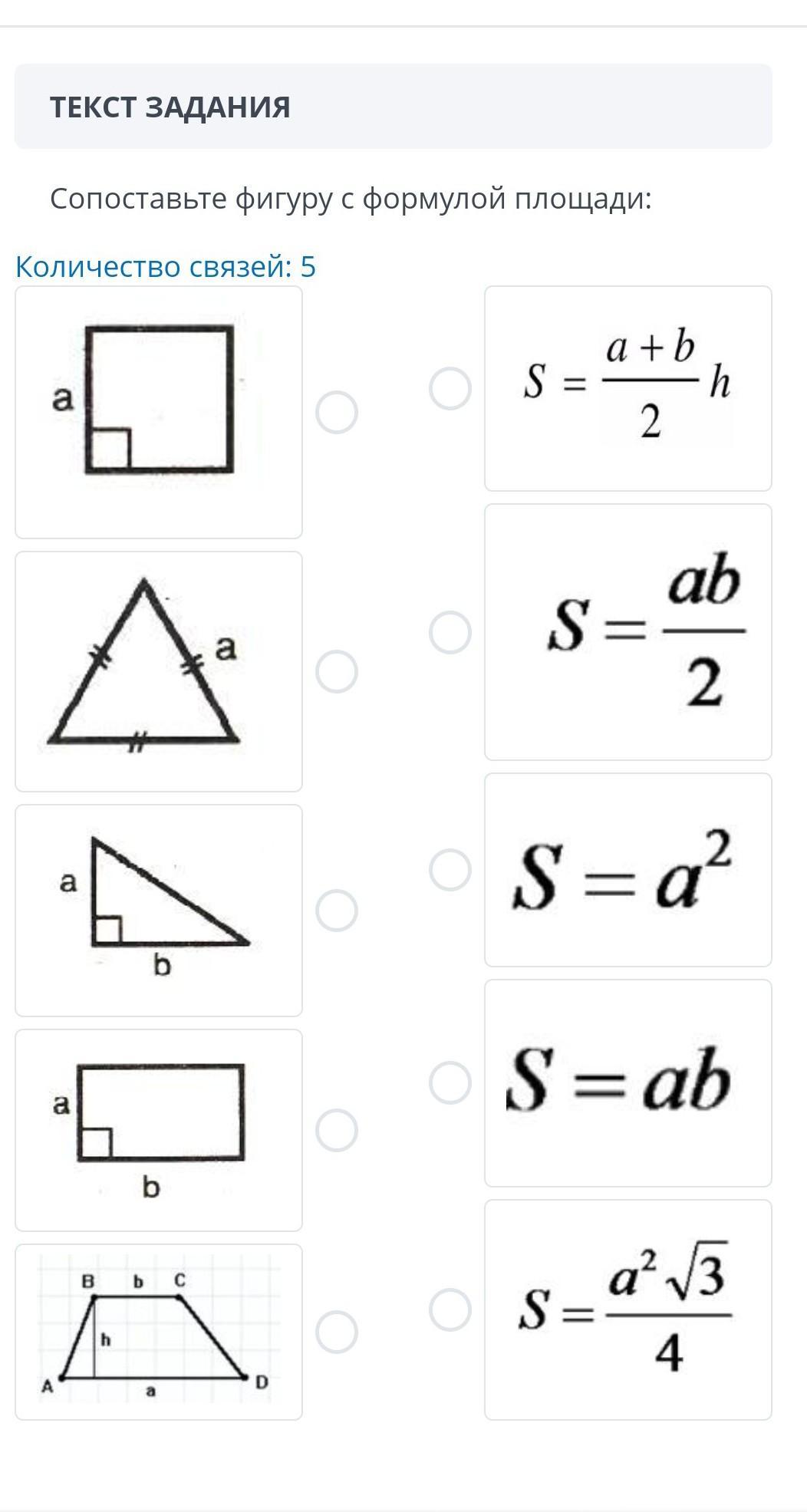
• На 1 рисунке нарисован квадрат, где a - сторона квадрата.

Площадь квадрата равна квадрату его стороны:

$\bf S = a^{2}$

• На 2 рисунке нарисован равносторонний треугольник, где a - сторона треугольника.

Площадь равностороннего треугольника вычисляется по формуле:

$\bf S = \dfrac{a^{2} \cdot \sqrt{3} }{4}$

• На 3 рисунке нарисован прямоугольный треугольник, где a и b - его катеты.

Площадь прямоугольного треугольника равна полупроизведению его катетов:

$\bf S = \dfrac{a \cdot b}{2}$

• На 4 рисунке нарисован прямоугольник, где a и b - его стороны.

Площадь прямоугольника равна произведению его смежных сторон:

$\bf S = a \cdot b$

• На 5 рисунке нарисована трапеция, где a - большее основание, b - меньшее основание, h - высота.

Площадь трапеции равна полусумме оснований, умноженной на высоту:

$\bf S = \dfrac{a+b}{2} \cdot h$