Предмет: Геометрия,
автор: BannedUser
ПОМОГИТЕ С ГЕОМЕТРИЕЙ!!!!!!!!!
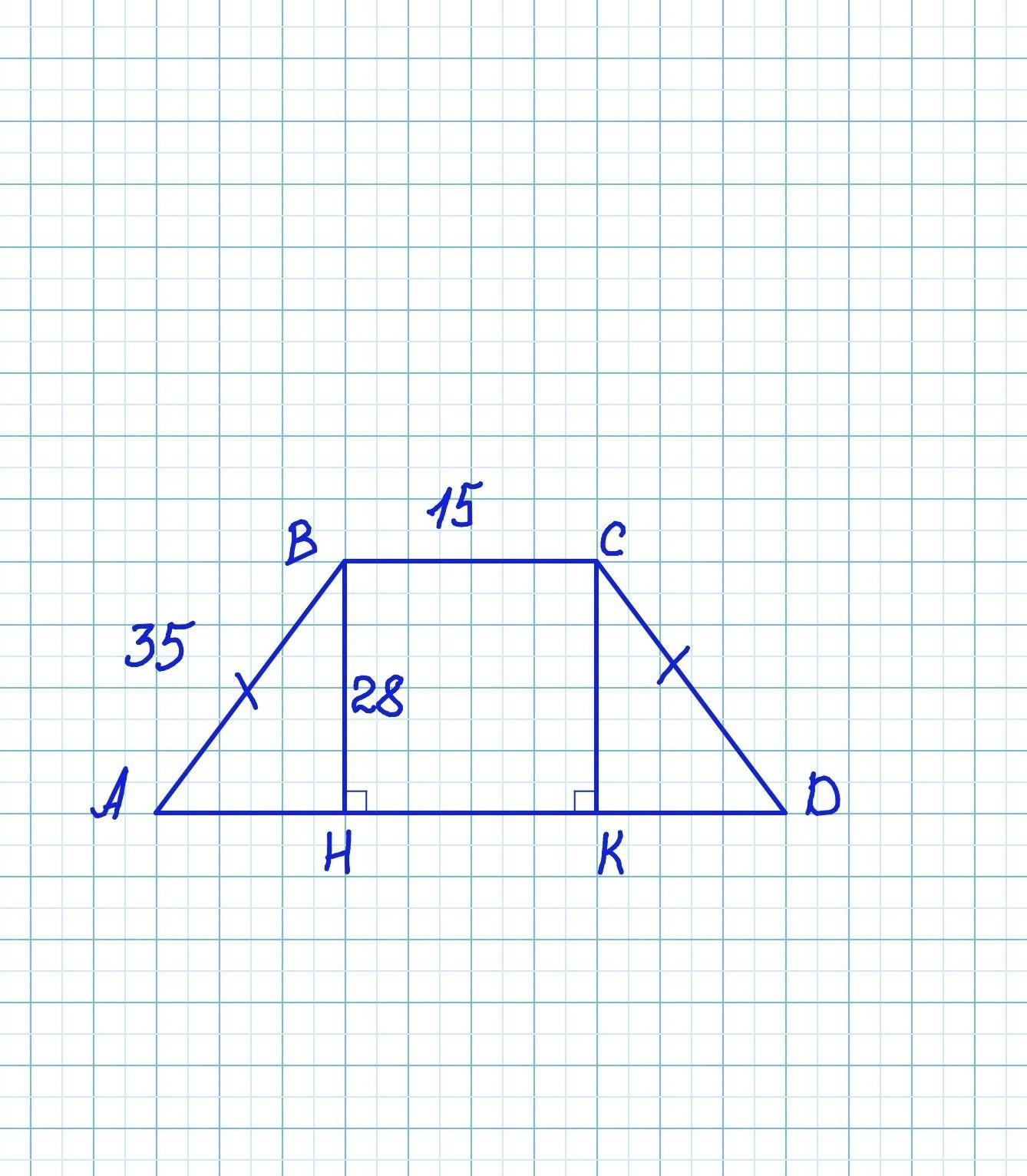
Высота равнобокой трапеции равна 28, а боковая сторона равна 35. Найди среднюю линию трапеции, если известно, что меньшее основание равно 15.
Аноним:
Теорема Пифагора √(35²-28²)=√(1225-784)=√441=21; нижнее основание 15+2*21=15+42=57. Средняя линия (57+15)/2=72/2=36
Ответы
Автор ответа:
0
Высота равнобокой трапеции равна 28, а боковая сторона равна 35. Найди среднюю линию трапеции, если известно, что меньшее основание равно 15.
Ответ:
36 см
Объяснение:
BH - высота, ВН⟂AD. Рассмотрим прямоугольный △АВН.
BH =28 ед, гипотенуза (она же боковая сторона трапеции) равна 35 ед.
По теореме Пифагора найдём катет АН:
АН=21 ед.
Так как трапеция равнобокая, то CD=AB=35 ед. СК=ВН=28 ед - как высоты трапеции. Следовательно прямоугольный △CKD равен прямоугольному △ВНА по гипотенузе и катету.
Из равенства треугольников следует: KD=AH=21 ед.
Нижнее основание равно: AD=AH+HK+KD.
HK=BC=15ед, как противоположные стороны прямоугольника ВСКН.
Поэтому AD=21+15+21=57 ед.
Длина средней линии трапеции равна полусумме длин оснований.
где а и b - основания трапеции.
Средняя линия трапеции равна 36 ед.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: za9999370
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: sewa1884
Предмет: Другие предметы,
автор: Kirynya
Предмет: Русский язык,
автор: НастВишневская