Предмет: Геометрия,
автор: kleverliker
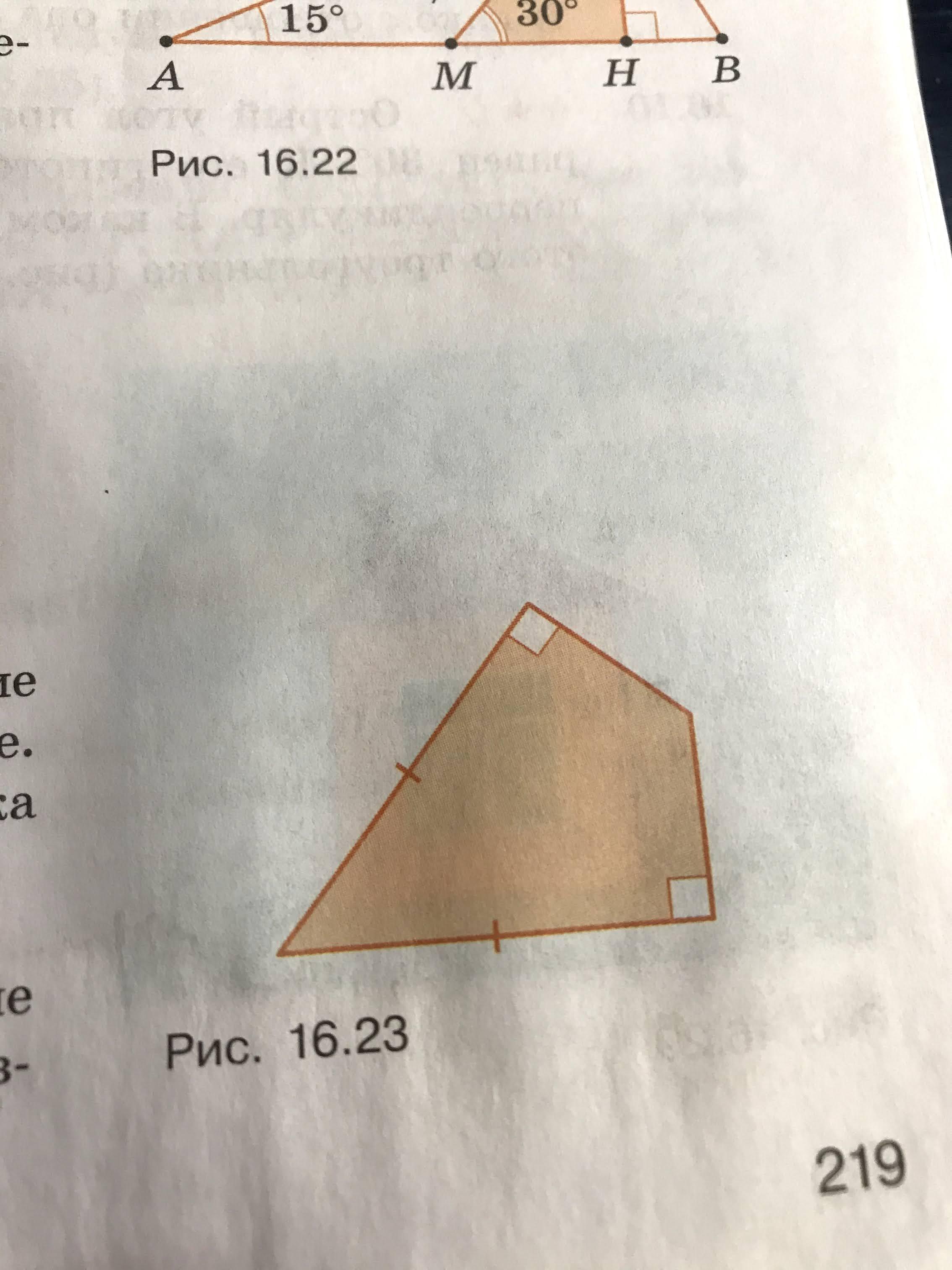
у четырех угольника равны две соседние стороны ,а два противоположных угла прямые. Докажите ,что диагонали этого четырех угольника взаимно перпендикулярны
Приложения:
Ответы
Автор ответа:
32
Ответ:
Объяснение:
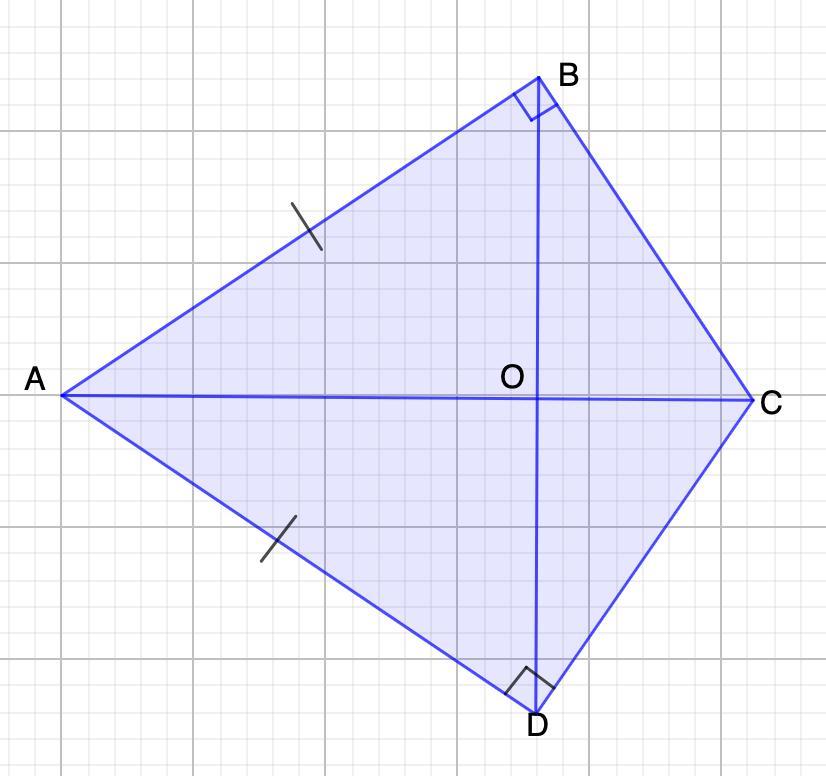
Дано: ABCD
∠В=∠D=90°
Доказать: АС⊥ВD
Доказательство:
Проведем диагонали АС и ВD.
1. Рассмотрим ΔАВС и ΔАСD = прямоугольные.
АВ=АD (условие)
АС - общая
⇒ ΔАВС = ΔАСD (по катету и гипотенузе)
⇒ ВС=СD;
∠ВСО=∠ОСD (как соответственные элементы)
2. Рассмотрим ΔВСD.
ВС=СD (п.1) ⇒ ΔВСD - равнобедренный.
∠ВСО=∠ОСD (п.1) ⇒СО - биссектриса, высота (свойство р/б Δ)
⇒ АС⊥ВD
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: mkryukov
Предмет: Русский язык,
автор: цветочекаленький11
Предмет: Беларуская мова,
автор: annashiloba2005
Предмет: Русский язык,
автор: ХитменАгент47