Предмет: Алгебра,
автор: maskskinsite
Интеграл. Проверьте правильно ли я решил
Приложения:
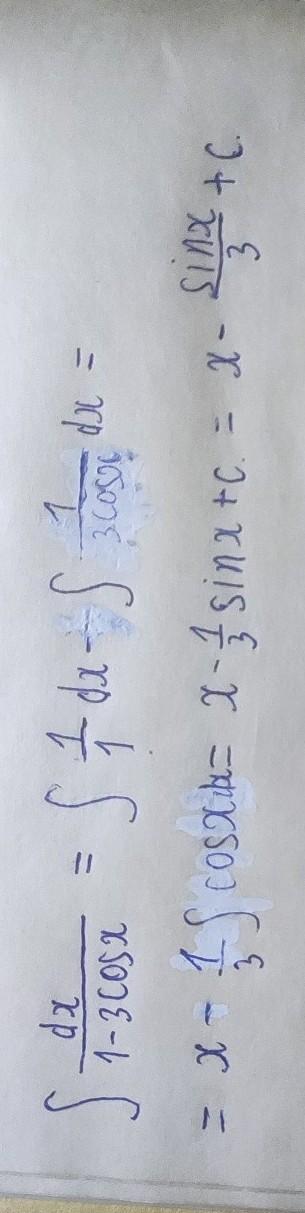
filuksistersp735lh:
найди производную своего ответа и проверь получится ли то что под знаком интеграла
очевидно что нет
Бывает решение правильное, а производная не совпадает
такого не бывает
значить наверное решение
потому что это обратные функции
Ответы
Автор ответа:
2
Используем универсальную тригонометрическую подстановку
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Українська література,
автор: торі2
Предмет: Другие предметы,
автор: DurgaQvop
Предмет: Английский язык,
автор: Beket2004