Предмет: Математика,
автор: igorbizn4
Помогите срочно надо пожалуйста
Приложения:
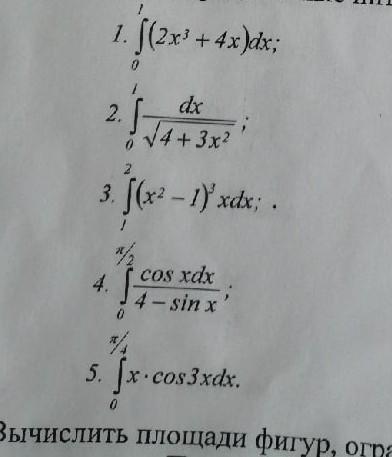
Ответы
Автор ответа:
4
1.
2.
3.
4.
5.
Решим неопределённый интеграл по частям:
Похожие вопросы
Предмет: Русский язык,
автор: 0402
Предмет: Русский язык,
автор: julya0320
Предмет: Қазақ тiлi,
автор: шалкаю
Предмет: Геометрия,
автор: Miroslaw2002
Предмет: Математика,
автор: Mr191