Предмет: Математика,
автор: totozao11
Найдите площадь фигуры ограниченная линиями
y=sqrt(x)
y=1
y=0
y=(x+2)^3
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
y=√x
y=(x+2)³
y = 1
y = 0
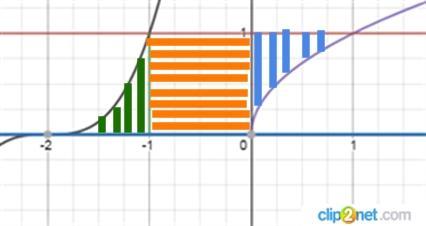
рисуем график и видим, что наша площадь состоит из трех площадей
1) х от -2 до -1 (y = (x+2)³; y = 0)
2) х от -1 до 0 (y=1; y=0)
3) х от 0 до 1 (y= 1; y = √x)
ищем три площади по отдельности
итого площадь искомой фигуры
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: erikhan81
Предмет: Английский язык,
автор: veracygankova
Предмет: Русский язык,
автор: liubotinskiir
Предмет: География,
автор: KraSava2281