Предмет: Математика,
автор: milaya139
Обчислити інтеграл застосовуючи потрібну заміну
Допоможіть будь ласка
Дуже потрібно
Приложения:
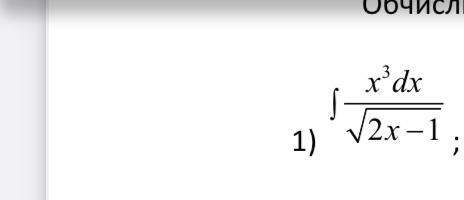
Ответы
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: медведь26рус1
Предмет: Русский язык,
автор: cavadbey
Предмет: Окружающий мир,
автор: комбин
Предмет: Алгебра,
автор: umar123345678910
Предмет: Биология,
автор: 228Mikhail228