Question

найти углы треугольника с полным решение м​

Answer 1

Ответ:

Теорема о внешнем угле треугольника:

Величина внешнего угла равна сумме углов треугольника, не смежных с ним.

То есть:

$\angle \: KED = \angle \: DFE + \angle \: EDF \\ x + 35^{\circ} = x - 15^{\circ} + 2x - 70^{\circ} \\ 2x = 35^{\circ} + 15^{\circ} + 70^{\circ} \\ 2x = 120^{\circ} \\ x = 60^{\circ} \\ \\ \angle \: DFE = 2 \times 60^{\circ} - 70^{\circ} = 50^{\circ} \\ \angle \: EDF = 60^{\circ} - 15^{\circ} = 45^{\circ} \\ \angle \: DEF = 180^{\circ} - 50^{\circ} - 45^{\circ} = 85^{\circ}$

Answer 2

Объяснение:

Внешний угол треугольника равен сумме двух оставшихся углов не смежных с этим внешним углом.

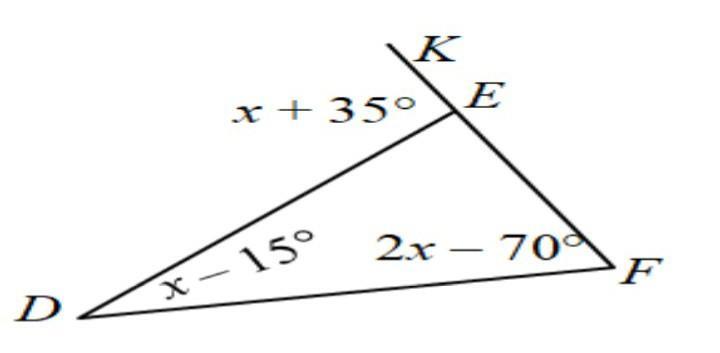
<DEK=<D+<F

Х+35=x-15+(2x-70)

X+35=x-15+2x-70

X-x-2x= - 70-15-35

-2x= - 120

X=60

<D=60-15=45

<F=2×60-70=120-70=50

<E=180-45-50=85

Ответ : <D=45 <F=50 <E=85