Предмет: Геометрия,
автор: redhizvp
В прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите площадь трапеции, если боковые стороны равны 8 см и 5см.
Ответы
Автор ответа:
1
Ответ:
10(16+√39) см²
Объяснение:
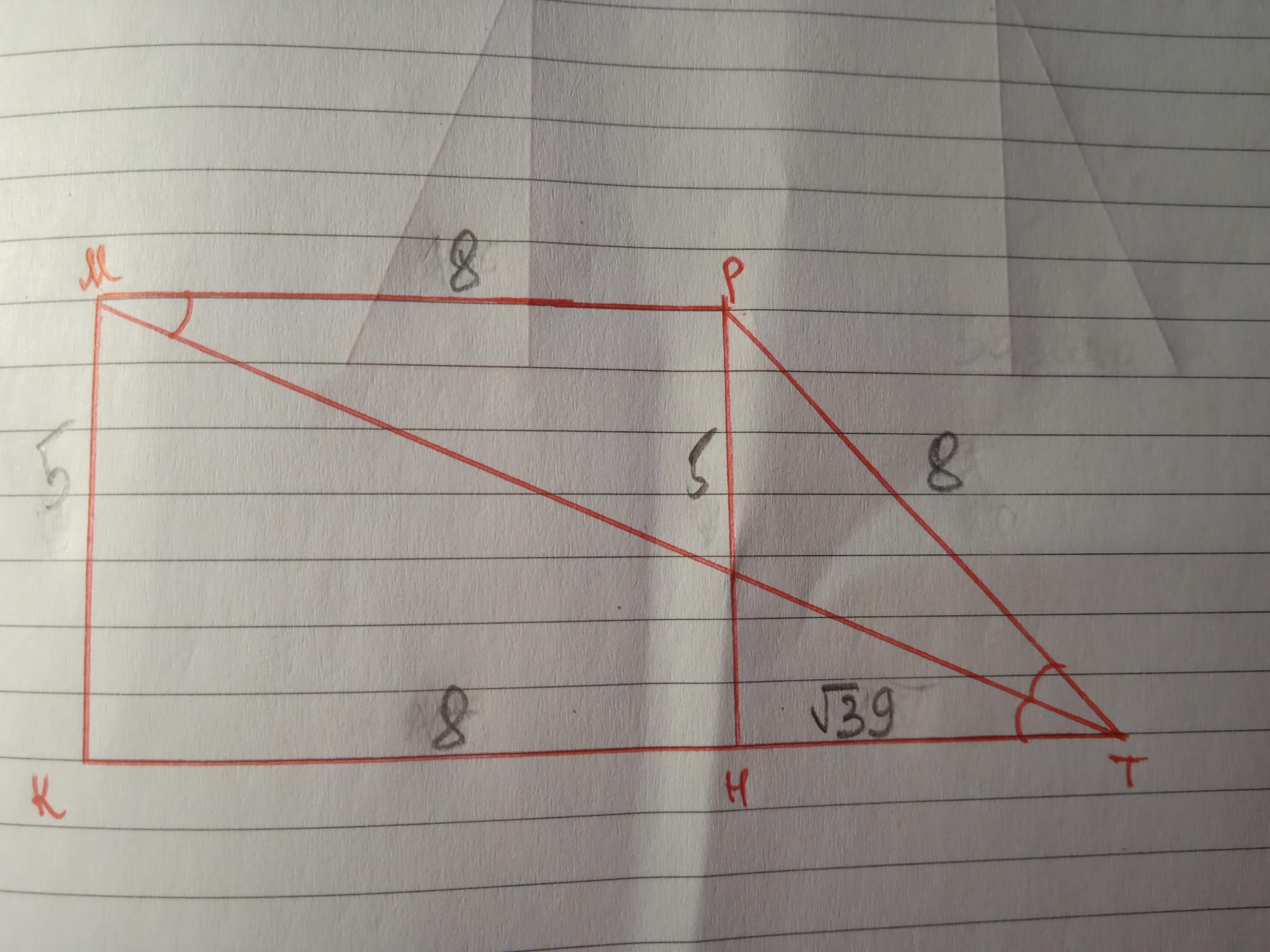
Дано: КМРТ - трапеция, МК⊥КТ, МК=5 см, РТ=8 см. МТ - биссектриса. Найти S(КМРТ).
∠КТМ=∠РТМ по определению биссектрисы
∠РМТ=∠МТК как внутренние накрест лежащие при МР║КТ и секущей МТ, значит ΔМРТ - равнобедренный, МР=РТ=8 см.
Проведем высоту РН=МК=5 см.
КН=МР=8 см.
ΔРТН - прямоугольный, РТ=8 см, РН=5 см, значит по теореме Пифагора ТН=√(64-25)=√39 см
КТ=КН+ТН=8+√39 см.
S=(МР+КТ):2*РН=(8+8+√39):2*5=10(16+√39) см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kigor07
Предмет: Технология,
автор: Аноним
Предмет: Русский язык,
автор: NuKuTa0609
Предмет: Биология,
автор: ilamanusko20
Предмет: Математика,
автор: abdulla9alievp53v8d