Question

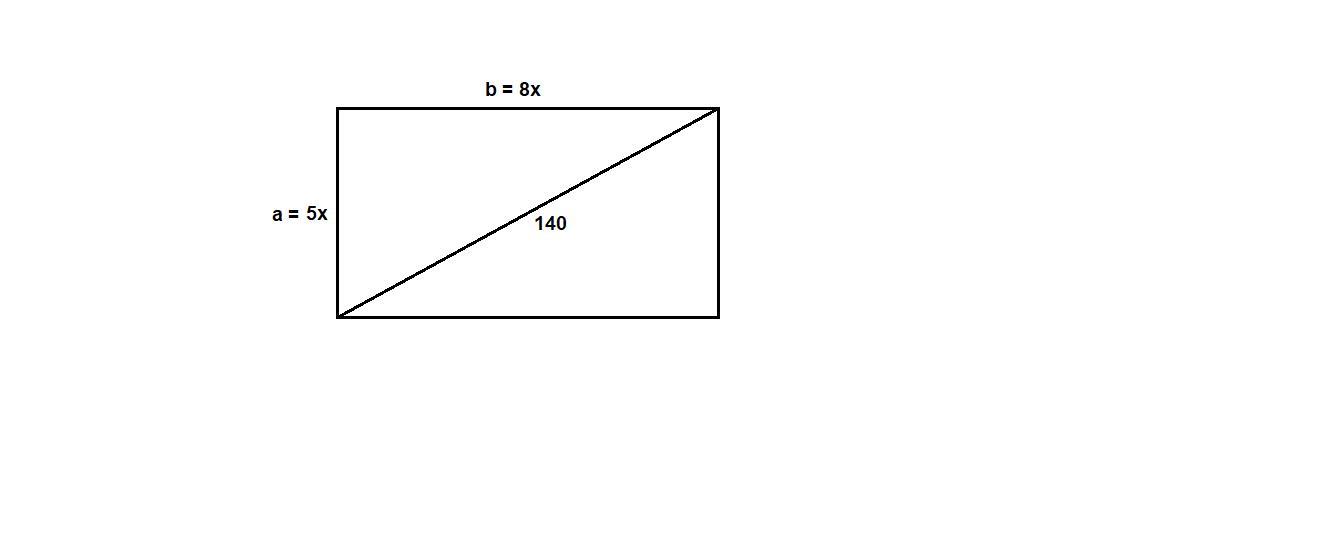
Прямоугольник.Соотношение сторон 16 к 10.Диагональ =140.Найти стороны 

Answer 1

Диагональ делит прямоугольник на два равных прямоугольных треугольника. По условию, стороны прямоугольника (а значит, катеты каждого из прямоугольных треугольников) относятся как 16/10=8/5.

Обозначим стороны прямоугольника (т.е. катеты треугольников) как 8х - большая и 5х - меньшая. По теореме Пифагора в прямоугольном треугольнике(стороны прямоугольника - катеты, диагональ - гипотенуза) получим:

(8х)"+(5х)"=140" (" означает возведение в квадрат)

64х"+25х"=19600

89х"=19600

х=140/?89   (? - квадратный корень)

Стороны соответственно равны:

8*140/?89=1120/?89

5*140/?89=700/?89

Ответ: стороны равны 1120/?89 и 700/?89 (можно избавиться от иррациональности в знаменателе, тогда получим: 1120*?89/89 и 700*?89/89)

(Есть второй способ решения через тангенс угла в этом же прямоугольном треугольнике, но по-моему, этот способ проще).

Answer 2

Ответ:

700√89 / 89

1120√89 / 89

Объяснение:

16/10 = 8/5

Пусть х - коэффициент пропорциональности. Тогда стороны треугольника 5х и 8 х.

По теореме Пифагора:

(5x)² + (8x)² = 140²

25x² + 64x² = 19600

89x² = 19600

x² = 19600 / 89

x = 140/√89

x = 140√89 / 89

a = 700√89 / 89

b = 1120√89 / 89