Question

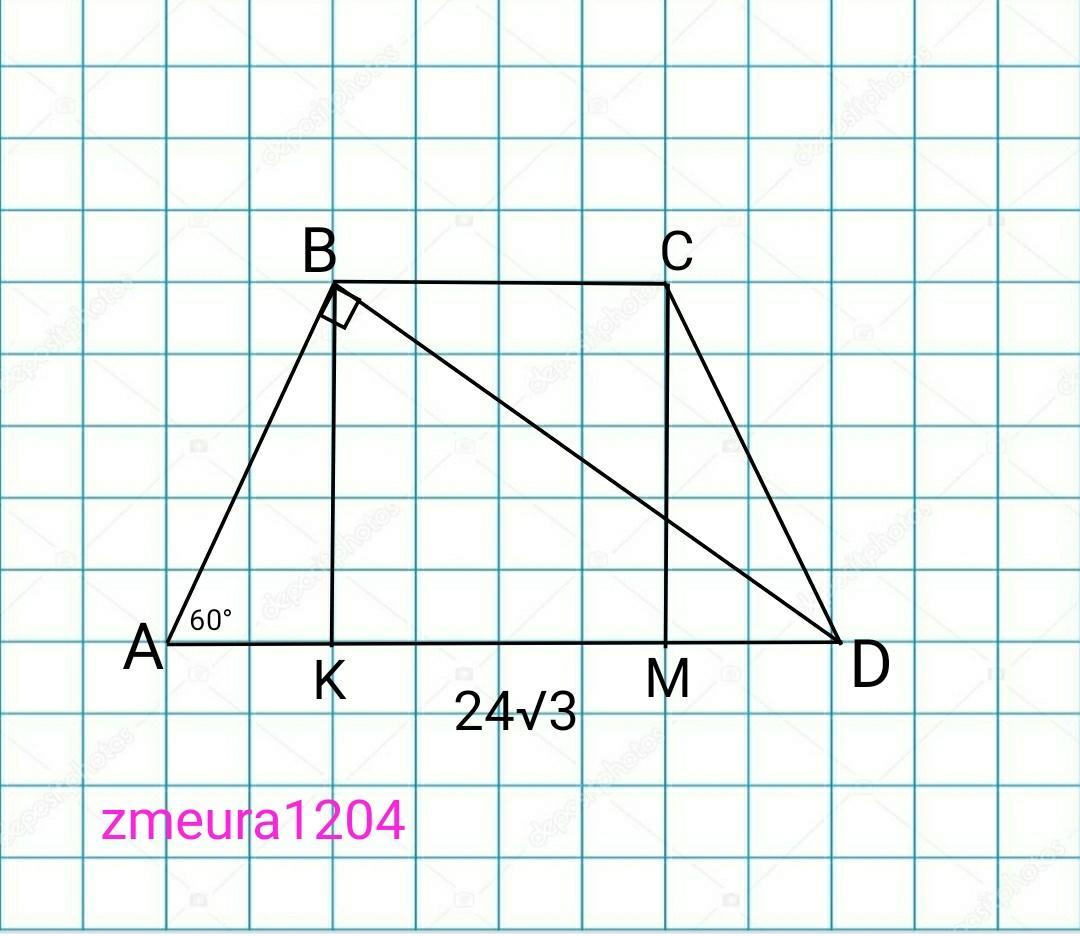
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите площадь трапеции если большое основание 24 корень из 3, а один из углов трапеции 60°​

Answer 1

Ответ:

324√3 ед²

Объяснение:

∆АВD- прямоугольный.

<А=60°

cos60°=1/2

cos<A=AB/AD

1/2=AB/24√3

AB=24√3/2=12√3 ед.

АВ²=АК*АD

AK=AB²/AD=(12√3)²/24√3=144*3/24√3=

=6√3ед

KD=AD-AK=24√3-6√3=18√3 ед

ВК=√(АК*КD)=√(6√3*18√3)=√324=18

ВС=KD-AK=18√3-6√3=12√3.

S=BK(BC+AD)/2=18(12√3+24√3)/2=

=18*36√3/2=324√3 ед²