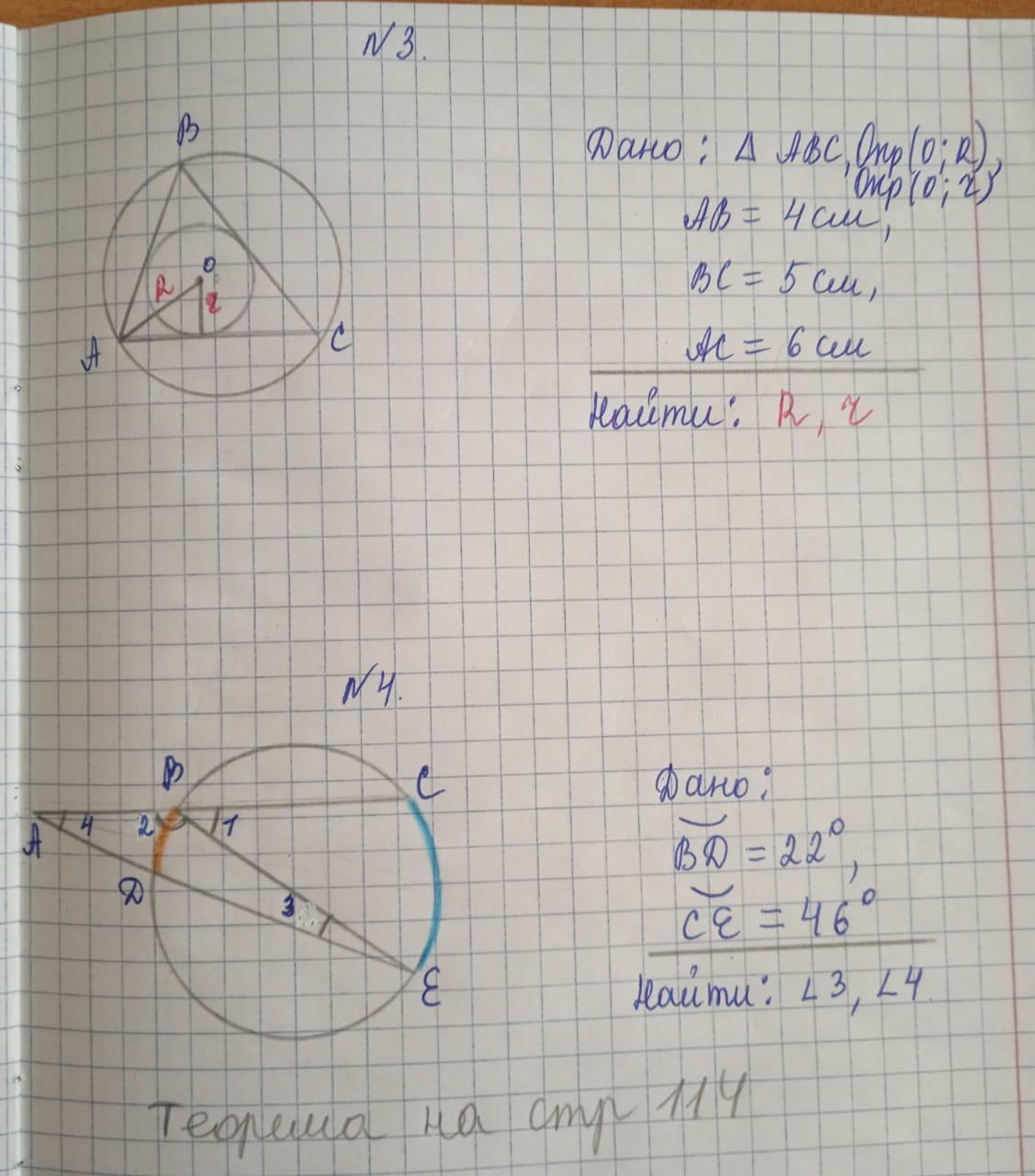
помогите решить 3.4 задачу
Ответы
Ответ:
Объяснение:
№3. Логика решения: для вычисления радиусов вписанной и описанной окружностей нужно знать все стороны треугольника и его площадь.
Для нахождения площади нужно знать высоту или синус угла между любыми сторонами.
Синус угла можно вычислить зная косинус этого угла.
Косинус угла можно найти по теореме косинусов.
Вычисления:
1. По теореме косинусов найдем косинус угла между сторонами 5 и 6 см:
4² = 5² + 6² - 2*5*6*Cosα
16 = 25 + 36 - 60*Cosα
Cosα = 45/60 или после сокращения дроби 3/4
2. Найдем значение синуса этого угла через основное тригонометрическое тождество:
Sinα = √(1 - Cos²α) = √(1 - 9/16) = √(7/16) = √7 / 4
3. Площадь треугольника = 1/2 * 5 * 6 * √7 / 4 = 15√7 / 4
4. Радиус вписанной окружности r = S / (a+b+c)/2
(a+b+c)/2 = 7.5
r = 15√7 / 4*7.5 = √7/2
5. Радиус описанной окружности R = a*b*c/4S = 4*5*6/15√7 = 8/√7 , но иррациональное выражение в знаменателе оставлять нельзя, поэтому окончательный ответ будет 8√7/7
№4 ∠ СВЕ вписанный, он равен половине дуги на которую опирается = 46/2 = 23°
∠ BED (∠3) тоже вписанный, = 22/2 = 11°
∠2 = 180 - ∠1 = 180 - 23 = 157°
∠4 = 180 - 157 - 11 = 12°