Предмет: Математика,
автор: bsmoon
Помогите пожалуйста.
Приложения:
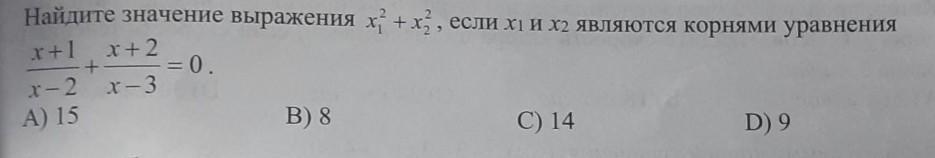
Ответы
Автор ответа:
2
Найдем корни уравнения:
x1 = ; х2 =
.
Найдем необходимое значение:
Подставим числовые значения:
Ответ: В) 8.
Похожие вопросы
Предмет: Русский язык,
автор: МиссКонфетка
Предмет: Русский язык,
автор: ndomaratskaya
Предмет: Английский язык,
автор: alvina2904
Предмет: Литература,
автор: niceekrem
Предмет: Математика,
автор: RealPlayer1