Предмет: Алгебра,
автор: vityamath
решите уравнение .........
Приложения:

Ответы
Автор ответа:
2
Ответ:
ОДЗ;
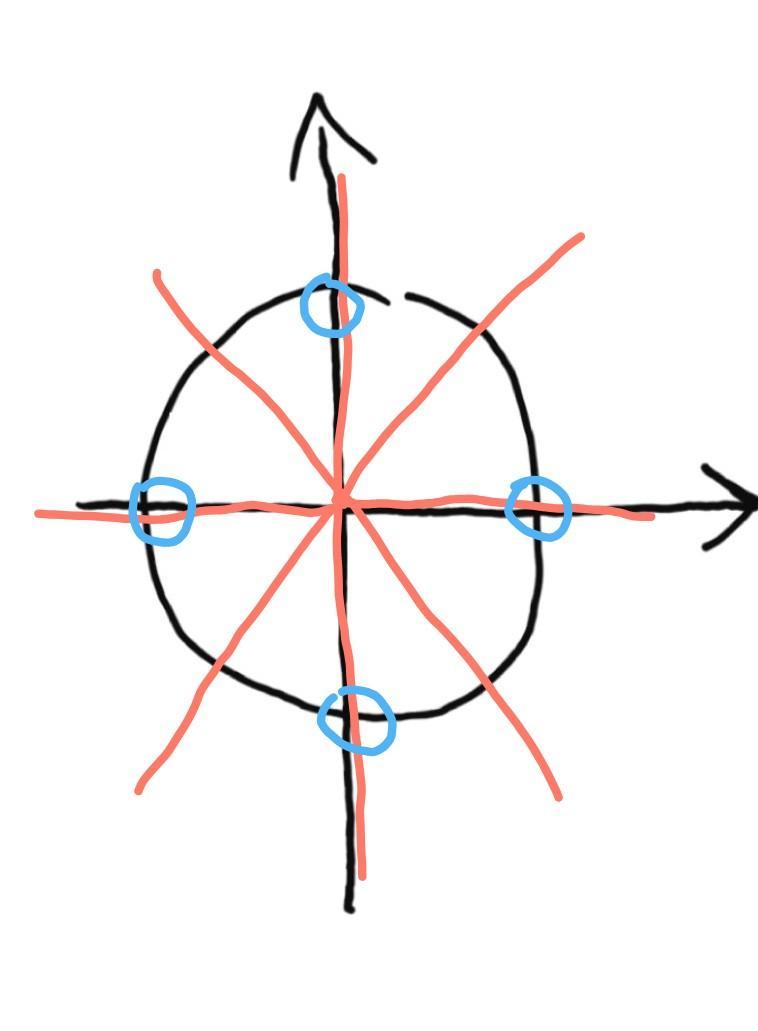
Рисунок:
красным отмечены корни числителя, синим - ОДЗ
Исключим синие корни и получим:
n принадлежит Z.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: vanechkasrgeev
Предмет: Русский язык,
автор: ekaterinaevmen
Предмет: Английский язык,
автор: Мухаметханова
Предмет: Русский язык,
автор: Маркетинг457
Предмет: Английский язык,
автор: катя5264