Основанием пирамиды является ромб, сторона которого равна 20 см и острый угол равен 30°.
Все углы, которые образуют боковые грани с плоскостью основания, равны 60°.
Вычисли высоту и площадь боковой поверхности пирамиды.
Высота пирамиды равна __ √3 см.
Площадь боковой поверхности равна __ см².
Ответы
Ответ:
см
см²
Объяснение:
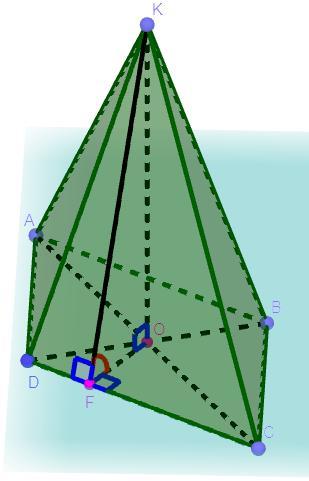
Дано: KABCD - пирамида, ABCD - ромб, CD = 20 см, ∠DCB = 30°
∠(ABC,KDC) = ∠(ABC,KBC) = ∠(ABC,KAB) = ∠(ABC,KAD) = 60°, OK ⊥ ABC
Найти:
Решение:
По теореме если все двугранные углы выпуклой пирамиды при ребрах равны, то проекцией вершины пирамиды на плоскость основания является центр вписанной окружности многоугольника, который есть основой пирамиды, тогда так как по условию все двугранные углы равны 60°, то точка K проектируется в точку O (по условию OK ⊥ ABC).
По свойствам ромба точка пересечения его диагоналей является центром вписанной окружности, то есть AC ∩ BD = O.
Из точки O проведем перпендикуляр стороне DC в точку F (плоскость ABC), то есть OF ⊥ DC. Соединим отрезком точки K и F.
По определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как OK ⊥ ABC по условию и OF ⊂ ABC по построению, то OK ⊥ FO, следовательно треугольник ΔKOF - прямоугольный.
По теореме о трех перпендикулярах KF ⊥ DC, так как OF ⊥ DC по построению, OK ⊥ FO и отрезок OF - проекция отрезка KF на плоскость ABC в прямоугольном треугольнике ΔKOF.
По определению углом между плоскостями, которые пересекаются называют тот двугранный угол, который принадлежит промежутку от 0° до 90° включительно, а по определению величиной двугранного угла называют величину его линейного угла, так как треугольник треугольник ΔKOF - прямоугольный, то угол ∠KFO < 90° и KF ⊥ DC, OF ⊥ DC, то угол ∠KFO - линейный угол двугранного угла между плоскостями KDC и ABC, то есть ∠KFO = ∠(ABC,KDC) = 60°.
По формуле площади ромба:
см².
По свойству ромба его диагонали делят ромб на четыре равные по площади треугольника, тогда см².
По формуле площади треугольника:
.
Рассмотрим прямоугольный треугольник ΔKOF.
По определению тангенса в прямоугольном треугольнике:
см.
По теореме если все двугранные углы выпуклой пирамиды при ребрах основания равны (по условию все двугранные углы равны 60°), то площадь боковой поверхности пирамиды можно вычислить по формуле:
см².