Question

Найдите основание равнобедренного треугольника, если
его боковая сторона равна корню из 3, а высота, опущенная на
основание, равна отрезку, соединяющему середину
основания с серединой боковой стороны Подсказка: связано сл средней линией​

Answer 1

Ответ:

3 см

Объяснение:

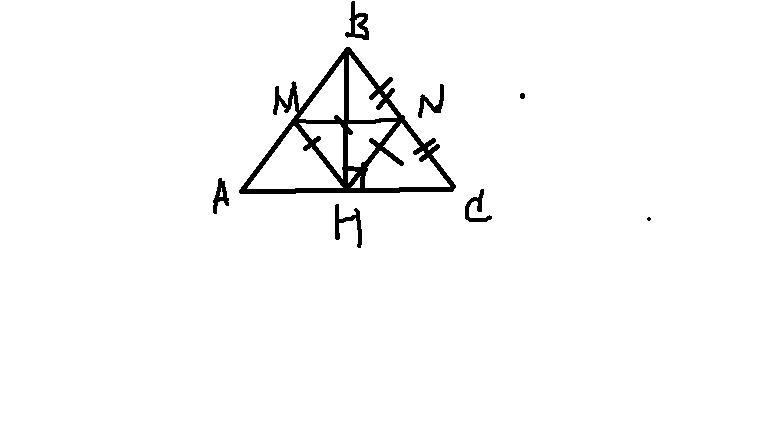
Отрезок, соединяющий середины боковых сторон треугольника - это средняя линяя, которая равна половине основания.

Как видно из рисунка, треугольник ABH - прямоугольный,

AM - это медиана, проведенная из прямого угла, и по свойству равна половине гипотенузе, значит, равна 0,5 * $\sqrt{3}$

Следовательно, треугольник HMB - равносторонний

По теореме Пифагора найдем его высоту MO ( я точку О не отметила), она же будет равна половине средней линии: Mo = $\sqrt{3/4 - 3/16} = \sqrt{ 9/16} = 3/4$

Средняя линяя MN = 6/4 = 3/2, значит, основание AC = 2 * 3/2 = 3

Answer 2

Условие запутало.

〰️Решение исправлено.

~Из-за того что отрезок соединяющий середину боковой стороны и середину основания, равна с высотой.

То высота равна половине стороны. То есть высота= корень3/2

Одна сторона корень 3, высота корень3/2.

В помощь приходит Пифагор!

По нему мы нашли один кусочек основания.

Одно основание равно 3/2 (=1,5)

Все же основание: 1,5+1,5=3

Ответ:3