Question

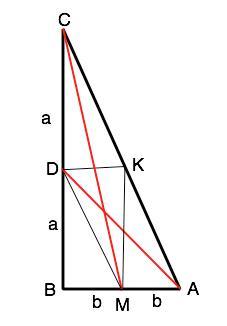
В прямоугольном треугольнике АВС СМ и АD – медианы, СМ=√156 и АD=√89 . Найдите гипотенузу АС.
РЕШАТЬ с корнями а не с приблизительными числами

Answer 1

Ответ: 14 (ед. длины)

Объяснение:

Примем ВD=CD=a;

BM=AM=b.

Проведем DK║AB,  KM║BD и DM║AC

DM, DK и КМ – средние линии ∆ АВС.=>

 DK=BM=AM=b

 KM=BD=DC=a.

DM=AK=CK

АКDM - параллелограмм.

СКМD - параллелограмм.

В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон.

Из ▱ АКМD

2b²+2DM²=a²+89 (1)

Из ▱ СКМD  

2a²+2DM²=b²+156 (2)

Сложив уравнения 1 и 2, получим:

2(а² +b²)+4 DM²=(a²+b²)+245⇒

(а² +b²)+4 DM²=(+245

Из ⊿ MBD a²+b²=DM²⇒

5DM² =245

DM²=49, DM=√49=7.

AC=2DM=14 (ед.длины)

————

Таким образом мы вывели одно из свойств медианы прямоугольного треугольника:  

• Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника, равна пяти квадратам медианы, опущенной на гипотенузу. А медиана такого треугольника из вершины прямого угла равна половине гипотенузы.

   Если знать и помнить это свойство, решение данной задачи сводится к одному лишь уравнению:

 5DM²=СМ²+AD²=245, откуда DM=7.

В прямоугольнике ВDКМ диагонали равны. Следовательно, медиана ВК=DM и AC=2DM=14.