Предмет: Геометрия,
автор: anohindima2018
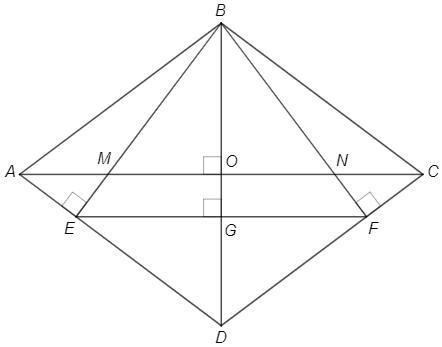
Из вершины тупого угла В ромб АВСD опущены перпендикуляры ВЕ и ВF на стороны АD и DС, пересекающие диагональ АС в точках М и N. Точка Е соединена с точкой F. Определите площадь MNFE, если диагонали ромба равны 160 и 120.
Ответы
Автор ответа:
1
Ромб - стороны равны, противоположные углы равны, диагонали перпендикулярны.
Треугольники ABE и CBF равны по гипотенузе и острому углу, AE=CF.
Точки E и F делят стороны ромба в равном отношении => AC||EF => EF⊥BD
S(ABO) =1/4 S(ABCD) =1/4 *1/2 *160*120 =2400
AB =√(AO^2 +BO^2) =100
∠ABD=∠ADB => △ABO~△BDE
BE/AO =BD/AB => BE =80*120/100 =96
△BEG~△BMO~△BDE => △BEG~△BMO~△ABO
S(BEG)/S(ABO) =(BE/AB)^2 =(96/100)^2 =0,96^2
S(BMO)/S(ABO) =(BO/AO)^2 =(60/80)^2 =0,75^2
S(MOGE) =S(BEG)-S(BMO) =2400 (0,96^2 -0,75^2) =861,84
S(MNFE) =2 S(MOGE) =1723,68
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: gannashmiger
Предмет: Українська мова,
автор: innakosto
Предмет: Английский язык,
автор: AnnaKeehl
Предмет: Химия,
автор: Золушка0307
Предмет: Алгебра,
автор: imbisimbis