Решите уравнения с помощью систем (хотя бы ответы дайте)
70 баллов
Заранее спасибо
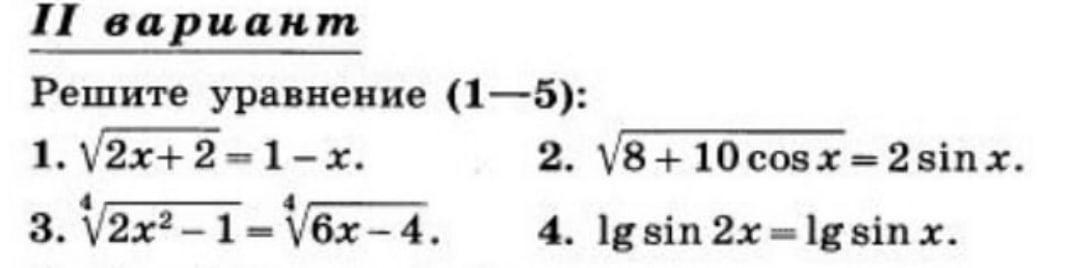
Ответы
1) Одз: 2х+2›=0 и 1-х›=0 т.е. -1‹=х‹=1
Возводим обе части в квадрат:
2х+2=1-2х+х^2
х^2-4х-1=0
х=2+√5(больше 1, не соответствует одз) или х=2-√5(это примерно -0,23)
Ответ: 2-√5
2) Одз: 8+10cosx›=0 и 2sinx›=0, т.е cosx›=-4/5 и sinx›=0
Возводим обе части в квадрат и делим на 2:
4+5cosx=2(sinx)^2
4-2(sinx)^2+5cosx=0
2(cosx)^2+5cosx+2=0
cosx=-1/2 или cosx=-2(не соответствует области значений cosx)
Значит
x=2pi/3+2pi*k или x=-2pi/3+2pi*k(sinx‹0, не соответствует одз), где k-целое
Ответ: x=2pi/3+2pi*k, где k-целое
3) Одз: 2х^2-1›=0 и 6х-4›=0
т.е. (х›=1/√2 или х‹=-1/√2) и х›=2/3, а значит
х ›= 1/√2(1/√2 всё же больше 2/3, это видно при возведении в квадрат)
Возводим обе части в 4 степень:
2х^2-1=6х-4
2х^2-6х+3=0
х=(3+√3)/2 или х=(3-√3)/2(не соответствует одз)
Ответ: (3+√3)/2
4) Одз: sinx›0 и sin2x›0, т.е sinx›0 и 2sinxcosx›0, а значит: sinx›0 и cosx›0(1 четверть тригонометрического круга)
Переносим по свойству логарифмов
lgsin2x-lgsinx=0
lg(sin2x/sinx)=0
sin2x/sinx=1
sin2x=sinx
2sinxcosx=sinx
2cosx=1
cosx=1/2
x=pi/3+2pi*k или x=-pi/3+2pi*k(не лежит в 1 четверти, не соответствует одз), где k-целое
Ответ: pi/3+2pi*k, где k-целое