Предмет: Геометрия,
автор: doctressa
1. Из точки, взятой на расстоянии 12см от прямой, проведены к ней две наклонные. Найдите расстояние между основаниями наклонных, если их сумма равна 28см,а проекции наклонных относятся как 5 :9.
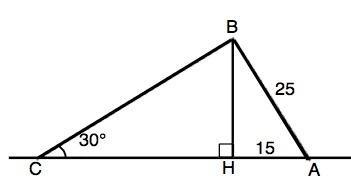
2.Из точки вне прямой проведены к ней две наклонные;длина одной из них равна 25 см, а длина ее проекции —15см. Найдите длину второй наклонной, если она образует прямой угол 30°.
Ответы
Автор ответа:
1
Ответ:
2) Расстояние от данной точки В до прямой равно длине проведенного к ней перпендикуляра ВН. Отрезок ВН - перпендикулярен прямой и является катетом треугольников, в которых наклонные – гипотенузы.
Из ∆АВН по т.Пифагора
ВН=√(ВА²-АН²)=√625-225)=20 см.
Из ∆ВСН: Катет ВН противолежит углу 30°. Синус 30°=1/2
Поэтому наклонная ВС=BH:sin30°=20:(1/2)=40 см
Можно просто вспомнить, что в прямоугольном треугольнике длина гипотенузы в два раза больше катета, лежащего против угла 30°⇒ ВС=2•20=40 см
Приложения:
Похожие вопросы
Предмет: Французский язык,
автор: voronkovanasty
Предмет: Русский язык,
автор: xdaijan
Предмет: Русский язык,
автор: masalimova1970
Предмет: Математика,
автор: AlisaCat29
Предмет: Химия,
автор: bohdanova24v