Question

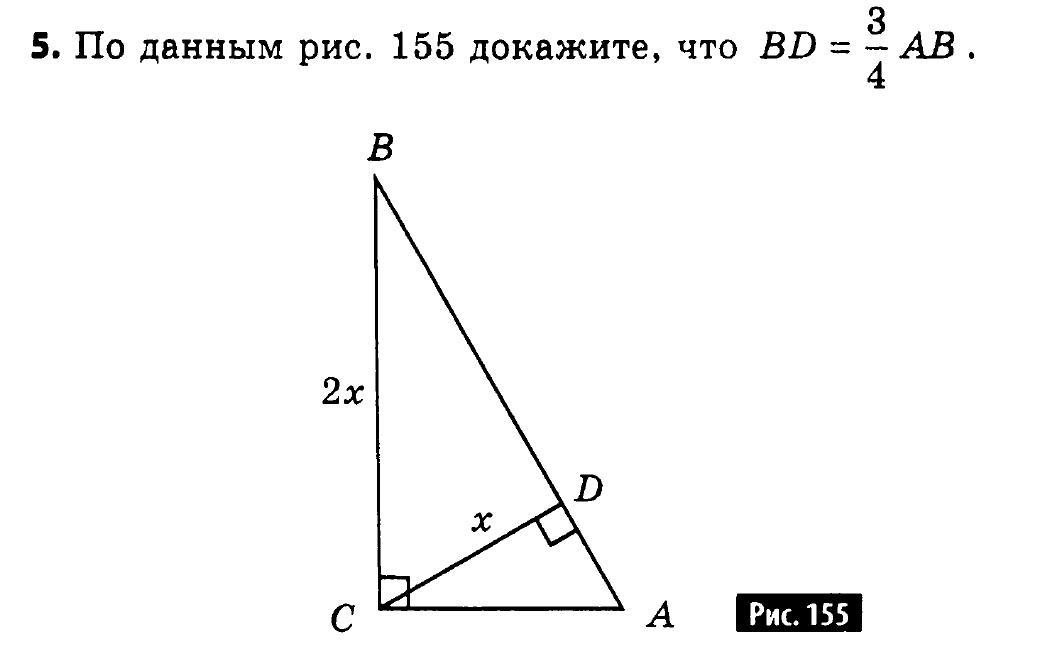
Решить задачу по теме "Прямоугольные треугольники".

Answer 1

Ответ:

ВD=3/4 АВ

Объяснение:

Если СD=x, а BC=2x

Получается, что угол В=30 градусов (катет, лежащий против угла в 30 градусов, равен половине гипотенузы)

СА-половина АВ

Тогда угол ВСА=60 градусов (180 - (90+30) =60)

В итоге угол DСА=30 градусов (90-60=30)

Выше было, что катет, лежащий против угла в 30 градусов, равен половине гипотенузы

Получается AD - половина СА, но СА- половина АВ

и с этого получается, что ВD=3/4 АВ

Answer 2

Ответ:  BD = 3/4 AB, что и требовалось доказать.

Объяснение:

Решение.

Из треугольника ВСD  BD = √(2x)²-x²= √4x²-x² = √3x² = x√3;

BD=x√3;

Так как СВ в 2 раза меньше В то угол В=30*. Следовательно угол А=60* и угол ACD = 30*.

Найдем AB = BC/cos30* = 2x : √3/2=4x/√3 = 4x√3/3;

 Найдем отношение BD к AB:

 BD : АВ =  x√3 : 4х√3/3  =  x√3 * 3/ 4x√3 = 3/4.

  BD : АВ =3/4  или

BD = 3/4 AB, что и требовалось доказать.

------------

x√3