Предмет: Математика,
автор: nargizamirolimova200
помогите решить неопределенный интеграл
Приложения:
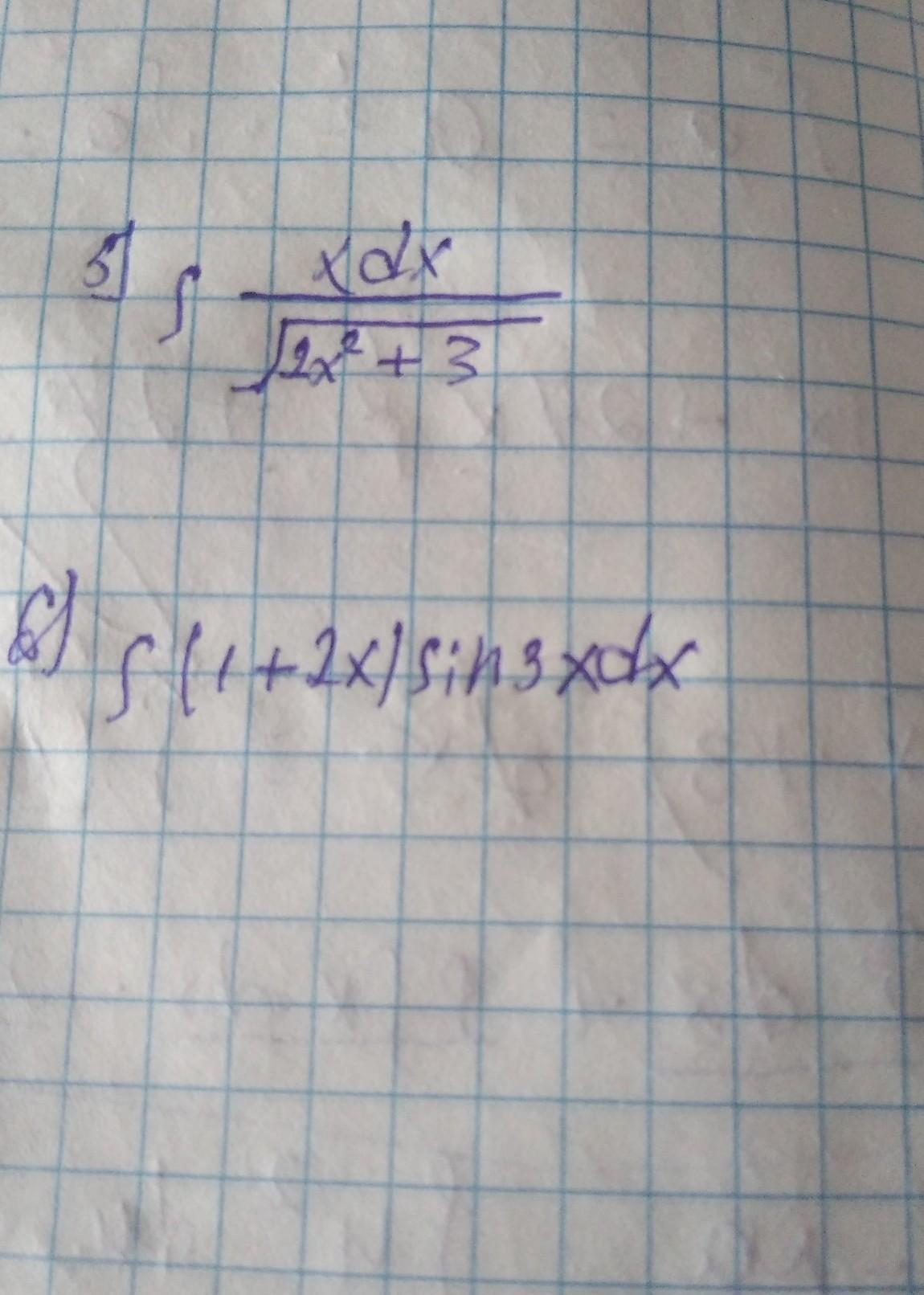
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
5)
6)
Похожие вопросы
Предмет: Английский язык,
автор: Каринучка
Предмет: Русский язык,
автор: Endera
Предмет: Русский язык,
автор: Katerinka721
Предмет: Математика,
автор: andreyaverya
Предмет: Английский язык,
автор: ястреб2288