Предмет: Математика,
автор: bralre345621
Помогите решить :
Нужно решить неопределенное интегралы
штук 5-7 на выбор
Приложения:
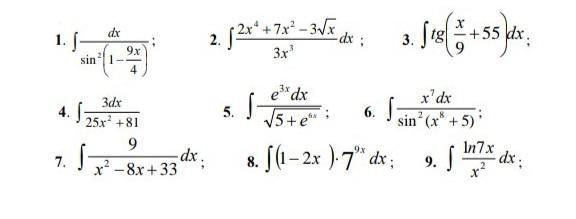
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
6.
7.
8.
Решаем по частям:
9.
По частям:
Похожие вопросы
Предмет: Русский язык,
автор: markikonnikovmark
Предмет: Русский язык,
автор: ana8772
Предмет: Русский язык,
автор: khauser
Предмет: Алгебра,
автор: Linkavitaminka24