Question

Произвольный треугольник имеет два равных угла. Третий угол в этом треугольнике равен 80°. Из равных углов проведены биссектрисы. Найди больший угол, который образовывается при пересечении этих биссектрис.

Answer 1

Ответ:

∠AOC = 130°

Объяснение:

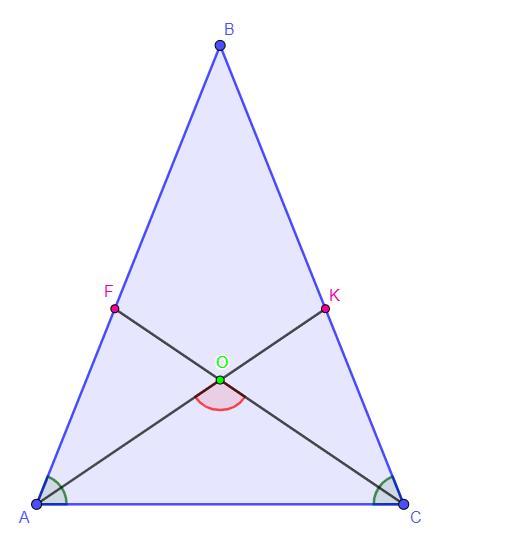
Дано: ∠BAC = ∠BCA, ∠ABC = 80°;AK,CF - биссектрисы; AK ∩ CF = O

Найти: ∠AOC - ?

Решение:

По теореме про суму углов треугольника (ΔABC):

∠BAC + ∠BCA + ∠ABC = 180° и так как по условию угол ∠BAC = ∠BCA, тогда угол ∠BAC = ∠BCA = 0,5(180° - ∠ABC) = 0,5(180° - 80°) =

= 0,5 · 100° = 50°.

По определению биссектриса делит угол пополам, тогда так как по условию AK,CF - биссектрисы, то:

∠KAC = ∠KAB = ∠BAC : 2 = 50° : 2 = 25°.

∠BCF = ∠ACF = ∠BCA : 2 = 50° : 2 = 25°.

По теореме про сумму углов треугольника (ΔAOC):

∠KAC + ∠FCA + ∠AOC = 180° ⇒ ∠AOC = 180° - ∠KAC - ∠FCA =

= 180° - 25° - 25° = 180° - 50° = 130°.