Предмет: Математика,
автор: Аноним
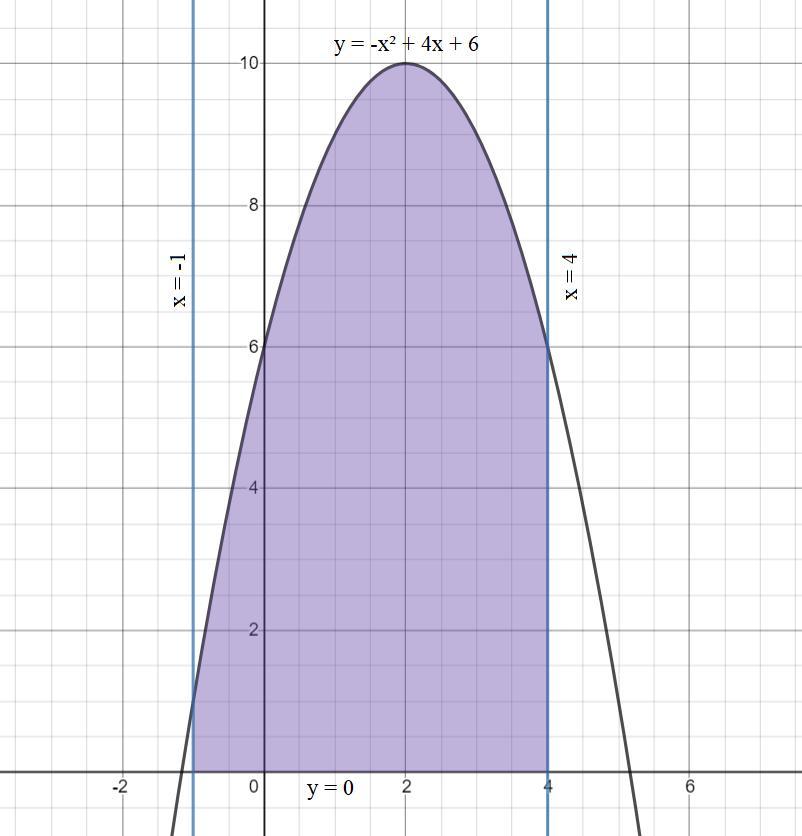
y=-x^2+4x+6,x=-1,x=4
Найти площадь криволинейной трапеции,ограниченную графиком функций
Ответы
Автор ответа:
1
Площадь криволинейной трапеции равна определённому интегралу f(x) - g(x) с границами интегрирования a и b:
Ответ: 38 1/3 квадратных единиц
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: IbChernousova
Предмет: Русский язык,
автор: Власова11
Предмет: Русский язык,
автор: профи4
Предмет: Русский язык,
автор: rail15
Предмет: Литература,
автор: shalobolov