Предмет: Математика,
автор: yehelem261
Найти производную функции
Приложения:
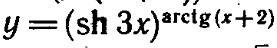
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: лизок71
Предмет: Русский язык,
автор: IbChernousova
Предмет: Русский язык,
автор: Власова11
Предмет: Английский язык,
автор: Иван0вто