Предмет: Алгебра,
автор: pavlovdanil04a
помогите пожалуйста
с полным решением
Приложения:
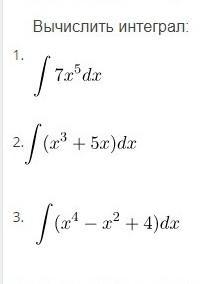
Ответы
Автор ответа:
0
Вычислить неопределённый интеграл значит найти общий вид первообразных для подынтегральной функции.
Важно помнить, что если , то общий вид первообразных будет
. Используя это, можно решить каждый из предложенных номеров.
1.
2.
3.
Похожие вопросы
Предмет: Другие предметы,
автор: Shegleva2015
Предмет: Русский язык,
автор: alenkaodegova
Предмет: Русский язык,
автор: sanyaglazunov
Предмет: Физика,
автор: shohida51
Предмет: Математика,
автор: jokerq1