Предмет: Алгебра,
автор: milenabulba
решите пожалуйста логарифмические неравенства
Приложения:
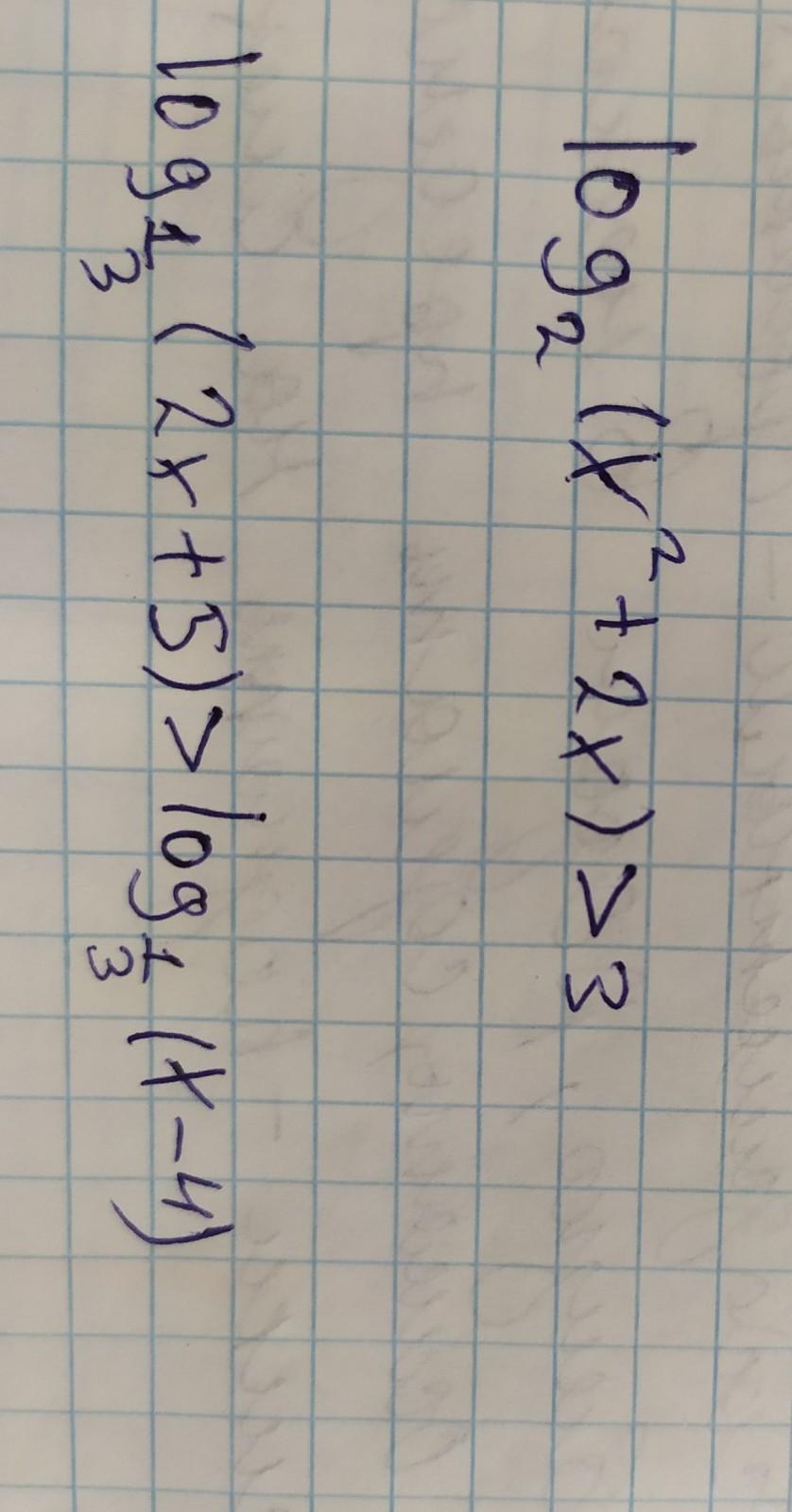
Ответы
Автор ответа:
0
Ответ:
а) x€ (-∞;-4)U(2;+∞)
б) x€∅
Объяснение:
N°1:
Т. к. основание логарифма 2 > основание 1 => знак неравенства не меняется
D = b²-4ac = 4+32 = 36 = 6²
х1= 2; х2 = -4
(х-2)(х+4) > 0
х€ (-∞; -4)U(2;+∞)
ОДЗ: х²+2х > 0
х(х+2) > 0
Значит:
х€ (-∞; -2)U(0;+∞)
Получаем систему:
{x€ (-∞;-4)U(2;+∞)
{x € (-∞;-2)U(0;+∞)
Отсюда:
x€ (-∞;-4)U(2;+∞)
Ответ: x€ (-∞;-4)U(2;+∞)
N°2:
Т. к основание логарифма 1/3 < основания 1 => знак неравенства меняется
2х+5 < х-4
х <-9
Значит:
х€ (-∞; -9)
ОДЗ:
{2х+5 > 0
{х-4 > 0
Получаем:
{х> -2,5
{х>4
Значит:
х€ (4;+∞)
Получаем систему:
{х€ (-∞;-9)
{х€ (4;+∞)
Отсюда: х€∅
Ответ: х€∅
Похожие вопросы
Предмет: Окружающий мир,
автор: 5657856
Предмет: Українська мова,
автор: babuwkanina
Предмет: Русский язык,
автор: VikaLunkina1
Предмет: Химия,
автор: poni5786
Предмет: Математика,
автор: фнаферотбога