Question

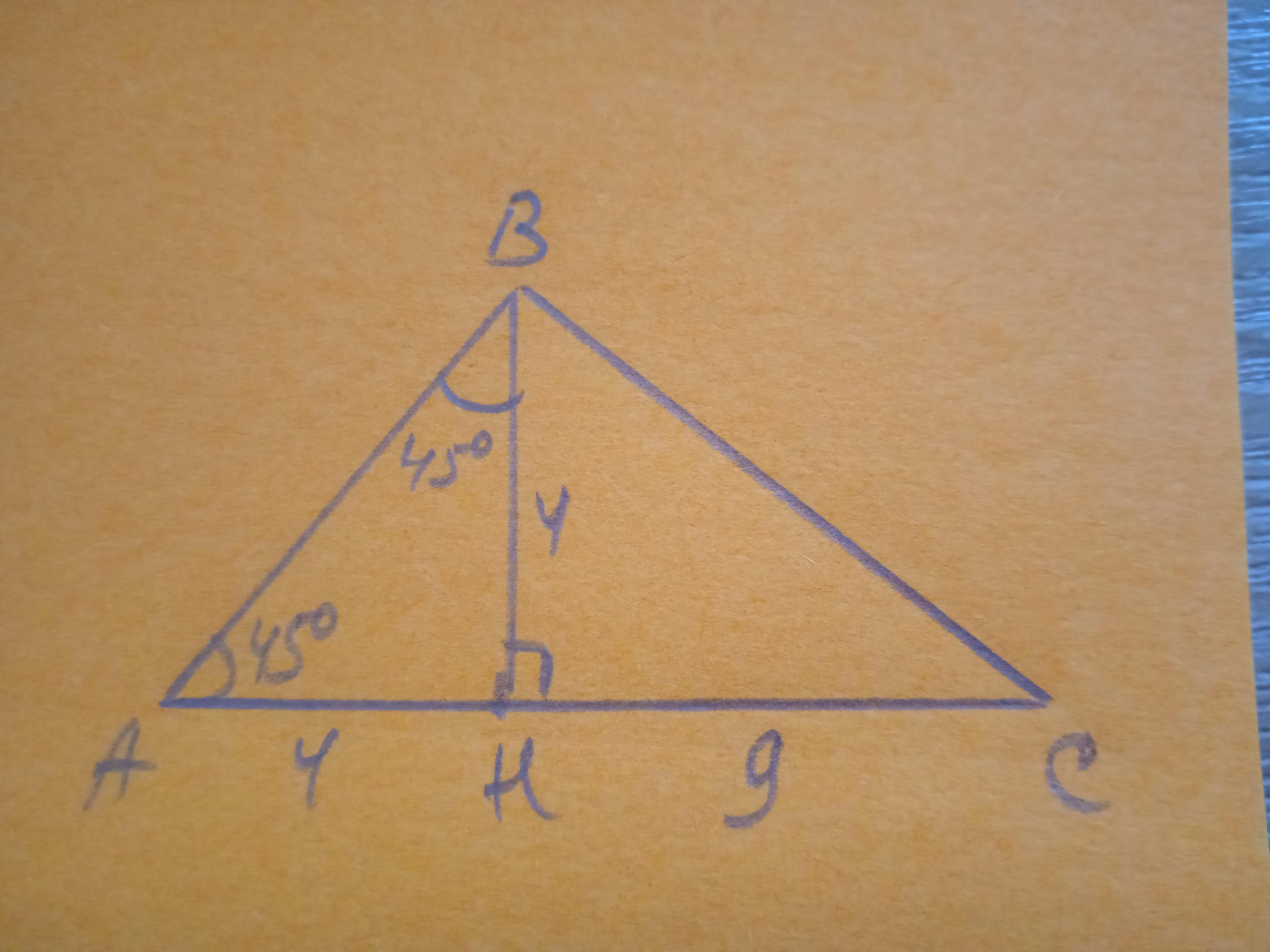
В треугольнике АВС, ∠А=45°, а высота ВН делит сторону АС на отрезки АН и НС соответственно равные 4 см и 9 см. Найдите площадь треугольника АВС.

Answer 1

Дано:

ΔАВС

∠А = 45°

AH = 4 см

НС = 9 см

Найти:

S - площадь ΔАВС

Решение:

Поскольку ∠А = 45°, а ВН ⊥ АС , то ΔАВН - прямоугольный равнобедренный треугольник, так как в нём

∠АВН = 90° - ∠А = 90° - 45° = 45°.

∠ АВН = ∠А = 45°.

ВН = АН = 4 см

BH - высота ΔАВС, а сторона АС, на которую опущена эта высота, равна

АС = АН + НС = 4 + 9 = 13 (см)

Тогда площадь Δ АВС

S = 0.5 ВН · АС = 0,5 · 4 · 13 = 26 (см²)

Ответ:

Площадь ΔАВС равна 26 см²

Answer 2

Ответ:

26 см²

Объяснение:

Дано: ΔАВС, ∠А=45°,  ВН - высота,  АН=4 см,  СН=9 см. Найти S(АВС).

Рассмотрим ΔАВН - прямоугольный, ∠АВН=∠А=45°, т.к. сумма острых углов прямоугольного треугольника 90°

АН=ВН=4 см

АС=АН+СН=4+9=13 см.

S(АВС) 1/2 * АС * ВН = 1/2 * 13*4=26 см²