Предмет: Алгебра,
автор: milenabulba
помогите пожалуйста! нужно решить логарифмические уравнения
Приложения:
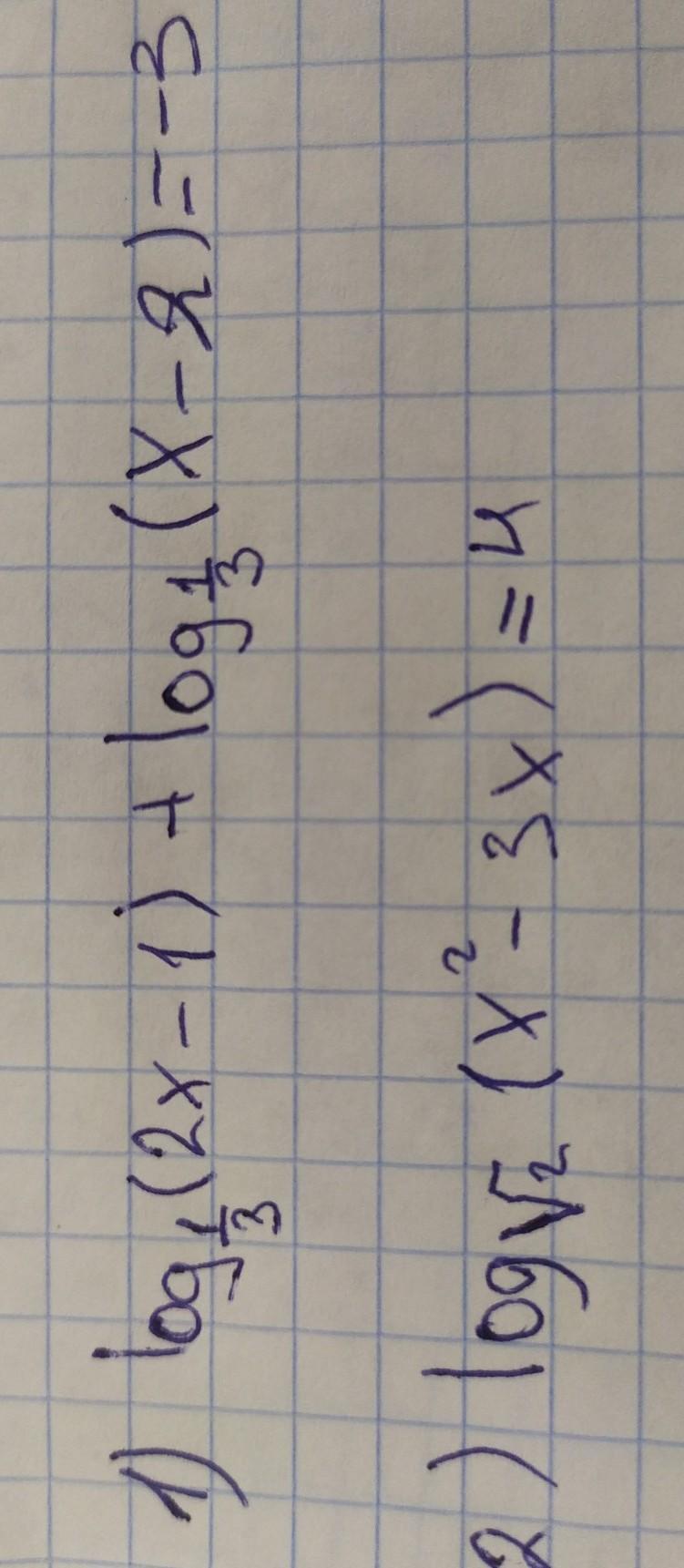
Miroslava227:
1 уравнение, второе слагаемое
log(x-?) какое число
x-2
Ответы
Автор ответа:
0
Ответ:
1.
ОДЗ:
корень -1 не подходит.
Ответ: 3.5
ОДЗ:
Ответ: -1; 4.
Похожие вопросы
Предмет: Русский язык,
автор: айган1
Предмет: Українська мова,
автор: anyazt
Предмет: Английский язык,
автор: Фурия222
Предмет: Другие предметы,
автор: Znaniesila2929
Предмет: Русский язык,
автор: Smithh