Question

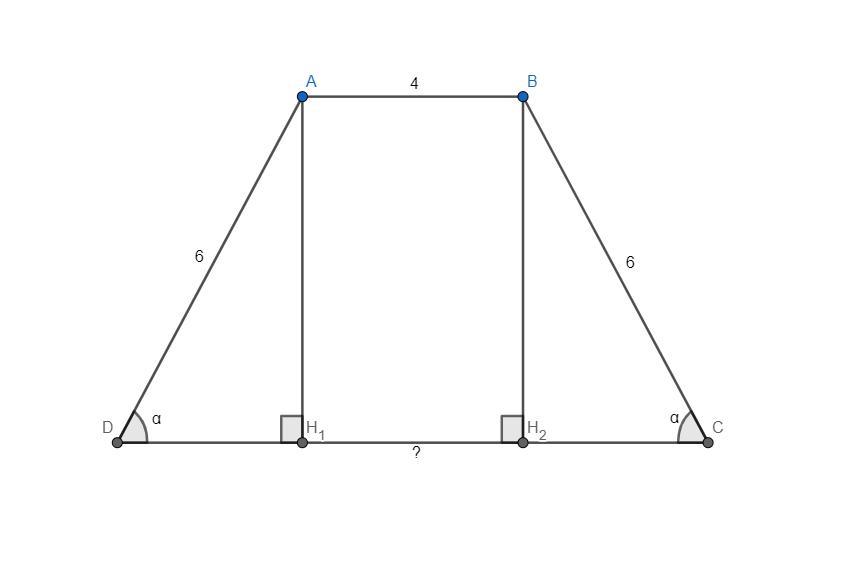
№1: В равнобокой трапеции меньшее основание равно 4 см, боковая
сторона равна 6 см, острый угол равен 56°. Найдите большее основание
трапеции. Ответ дайте в сантиметрах.
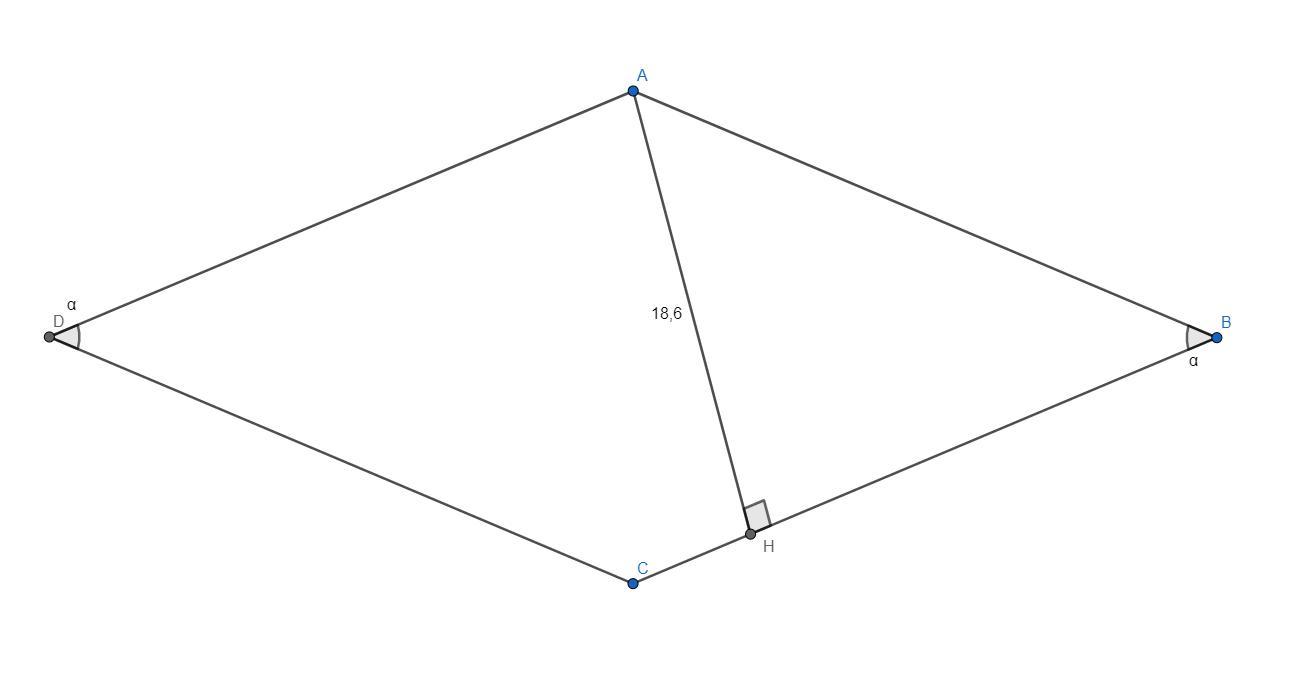
№2: В ромбе острый угол равен 37°, а высота равна 18,6 см. Найдите
сторону ромба. Ответ дайте в сантиметрах и округлите его до сотых.

Answer 1

Ответ:

$1)\ 10,72\\\\2)\ 11,19$

Объяснение:

$1)$

Дано: $\alpha = 56^{\circ},\,AB \parallel CD,\,AB = 4,\, BC=AD=6$

Найти: $CD\ -\ ?$

Решение:

Опустим высоты $AH_1,\, BH_2$ (см. рис 1). Тогда $H_1H_2=AB$ и $\triangle AH_1D,\,\triangle BCH_2$ - прямоугольные треугольники, так как

$H_1,\,H_2\in CD,\\\\AB \parallel CD,\\\\\angle AH_1D=\angle BH_2C=90^{\circ}$

Следовательно $cos\ 56^{\circ}=cos\ \angle C=cos\ \angle D=\frac{DH_1}{DA}=\frac{CH_2}{BC} \Rightarrow\\\\\Rightarrow DH_1=CH_2=DA\cdot cos\ 56^{\circ}=BC\cdot cos\ 56^{\circ}=6\cdot cos\ 56^{\circ}\approx3,36$

И тогда:

$CD = CH_2+H_2H_1+H_1D=2DH_1+AB=2\cdot 3,36+4=10,72$

Ответ: $CD = 10,72$

$2)$

Дано: $\alpha=37^{\circ},\,AB=BC=CD=DA,\,AH=18,6$

Найти: $AB,\,BC,\,CD,\,DA\ -\ ?$

Решение:

Треугольник ABH - прямоугольный, $\angle A = 37^{\circ},\, \angle H=90^{\circ}$.

Следовательно $sin\ \angle A=\frac{AH}{AB}\Rightarrow AB=AH\cdot sin\ \angle A=18,6\cdot sin\ 37^{\circ}\approx 11,19$

Ответ: $AB,\,BC,\,CD,\,DA=11,19$