Question

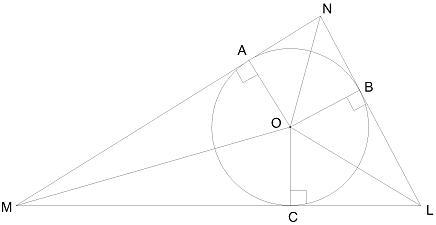
СРОООЧНО МАМА МЕНЯ УБЬЁТ В треугольник вписана окружность. Вычисли углы треугольника, если ∢ NMO= 36° и ∢ ONL= 40°. 12ok.png ∢ M= °; ∢ N= °; ∢ L= °.

Answer 1

Ответ:

∠M=72°  , ∠N=80°,  ∠L=28°

Решение:

Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Значит ∠М=2*∠NMO=2*36°=72°,

∠N=2*ONL=2*40°=80°

По теореме о сумме трёх углов треугольника найдём

∠L=180°-72°-80°=28°