Предмет: Математика,
автор: LadyMar1a
найдите производные с объяснением решения
Приложения:
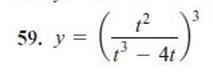
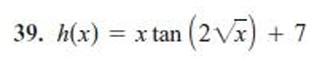
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: shvabsr
Предмет: Русский язык,
автор: тимоха23
Предмет: Қазақ тiлi,
автор: timur30102007
Предмет: Русский язык,
автор: ЕлизаветаДобрая