Question

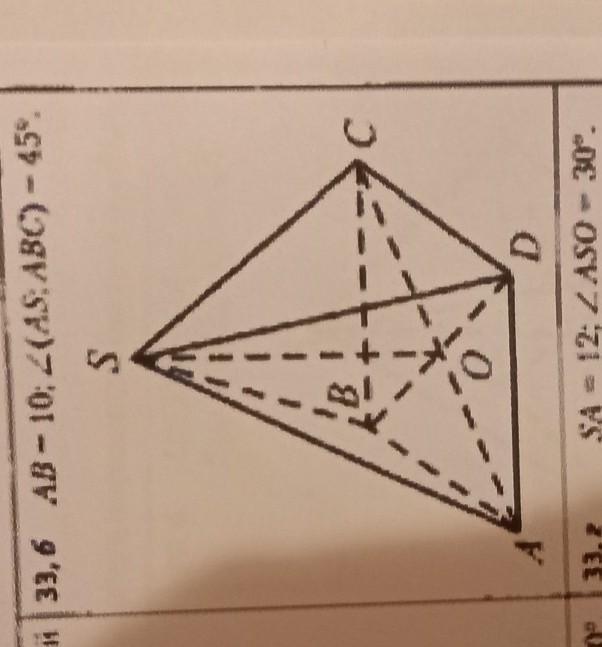
На рисунке изображена правильная пирамида. Найдите площадь полной поверхности пирамиды.
АВ=10, угол(AS,ABC)=45
срочно помогите

Answer 1

Пирамида SABCD правильная, значит, в основании лежит квадрат ABCD со стороной AB = 10. Диагональ квадрата:

AC = 10√2

Диагонали квадрата точкой пересечения делятся пополам:

AO = OC = AC : 2 = 10√2 : 2 = 5√2

Угол между прямой AS и плоскостью (ABC) - это угол между наклонной AS и проекцией AO этой наклонной на плоскость (ABC):

∠SAO = 45°

Высота пирамиды SO является катетом прямоугольного треугольника SOA, в котором:

∠SOA = 90°;  ∠ASO = ∠SAO = 45°.

Два угла в треугольнике равны, значит, ΔSOA - прямоугольный равнобедренный:

SO = AO = 5√2

Гипотенуза прямоугольного равнобедренного треугольника:

AS = AO · √2 = 5√2 · √2 = 10

Все боковые рёбра правильной пирамиды равны:

AS = BS = CS = DS = 10  и равны стороне квадрата в основании 10, значит, все 4 боковые грани пирамиды являются равносторонними треугольниками.

Площадь равностороннего треугольника со стороной $a$:

$S_{\triangle}=\dfrac {a^2\sqrt3}4$

Площадь полной поверхности пирамиды:

$S=4\cdot S_{\triangle ASD}+S_{ABCD}=\\\\=4\cdot \dfrac{AS^2\cdot \sqrt 3}4+AB^2=AS^2\cdot \sqrt3+AB^2=\\\\=10^2\cdot \sqrt 3+10^2\boldsymbol{=100(\sqrt3+1)}$

Ответ: 100(√3 + 1)