Предмет: Алгебра,
автор: Аноним
Помогите решить тригонометрические уравнения ,надо решить 10 штук пожалуйста очень надо(
Приложения:
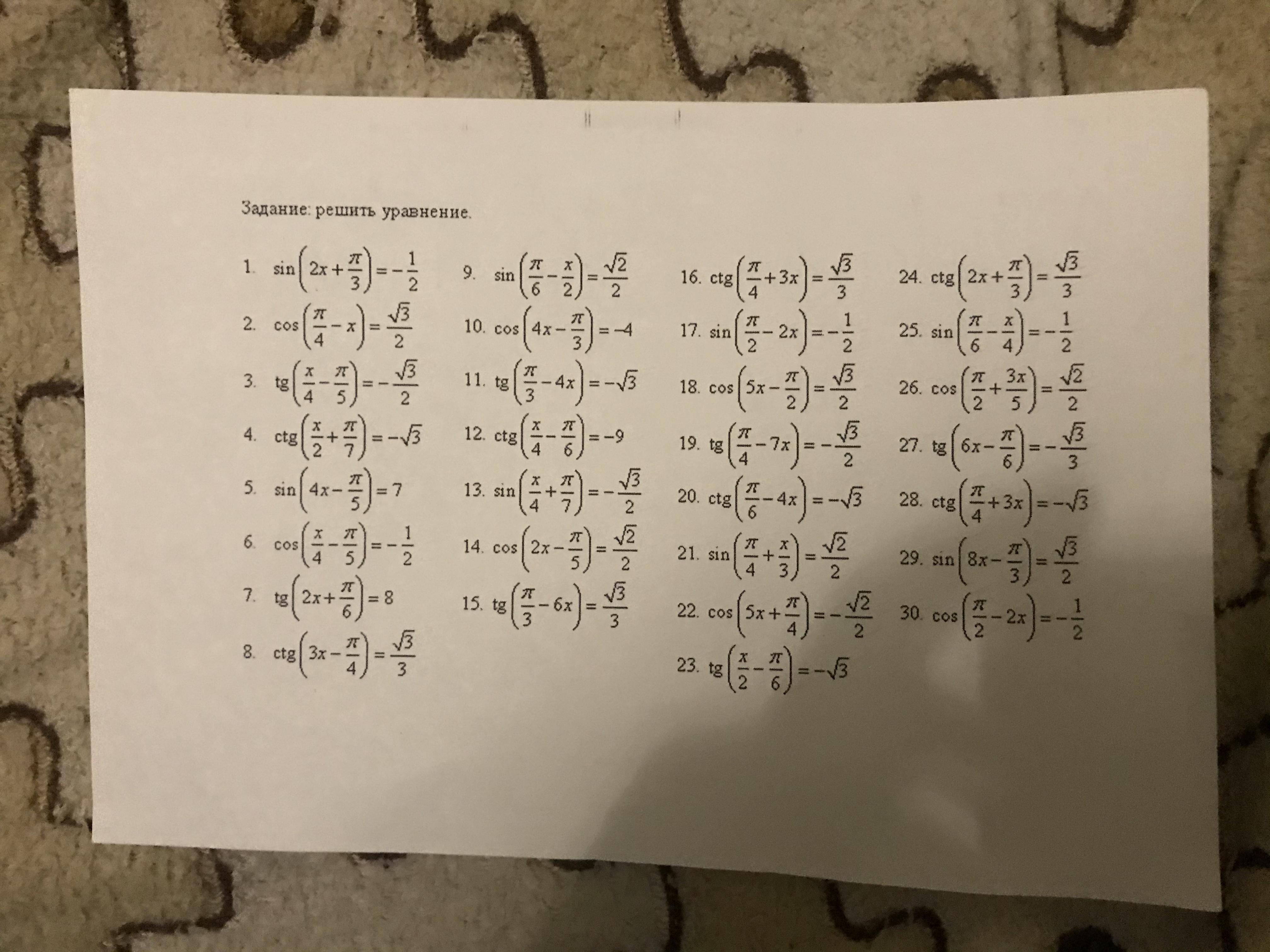
Ответы
Автор ответа:
0
Ответ:
1.
2.
3.
4.
5.
6.
7.
8.
11.
12.
везде n принадлежит Z.
Аноним:
А помоги пожалуйста решить sin(pi/6-x/4)=-1/2
Похожие вопросы
Предмет: Другие предметы,
автор: chukarev97
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: alfhis
Предмет: История,
автор: svelt04
Предмет: Алгебра,
автор: 234612