Предмет: Математика,
автор: bakcell4500
Выполните Действие
Выполните Действие
Приложения:
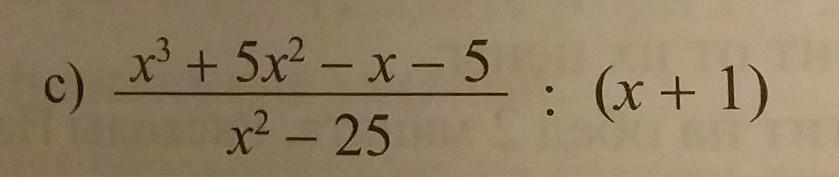
Ответы
Автор ответа:
2
-
-
-
D=36
-
-
Похожие вопросы
Предмет: Русский язык,
автор: abramianzar
Предмет: Русский язык,
автор: Ирина0518
Предмет: Русский язык,
автор: 7888868959
Предмет: Математика,
автор: rttyhh
Предмет: Химия,
автор: kylas2003