Предмет: Математика,
автор: mariabrо
Знайти інтеграли, застосувавши формулу інтегрування
частинами
Приложения:
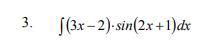
Ответы
Автор ответа:
0
Ответ:
По частям:
Похожие вопросы
Предмет: Русский язык,
автор: koshkarov92
Предмет: Английский язык,
автор: golofeevalenul
Предмет: Английский язык,
автор: kristinabezpal
Предмет: Биология,
автор: Дентсик901
Предмет: Английский язык,
автор: sua2