Предмет: Математика,
автор: mariabrо
Знайти визначений інтеграл
Приложения:
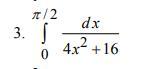
Ответы
Автор ответа:
1
Ответ:
DASASAD:
мне помогите пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: rotaru2000
Предмет: Русский язык,
автор: няшка371
Предмет: Русский язык,
автор: lobachev06
Предмет: Математика,
автор: oksa5505
Предмет: Математика,
автор: проансе