1. Используя информацию на рисунке, определите, параллельны ли прямые a и b или нет.
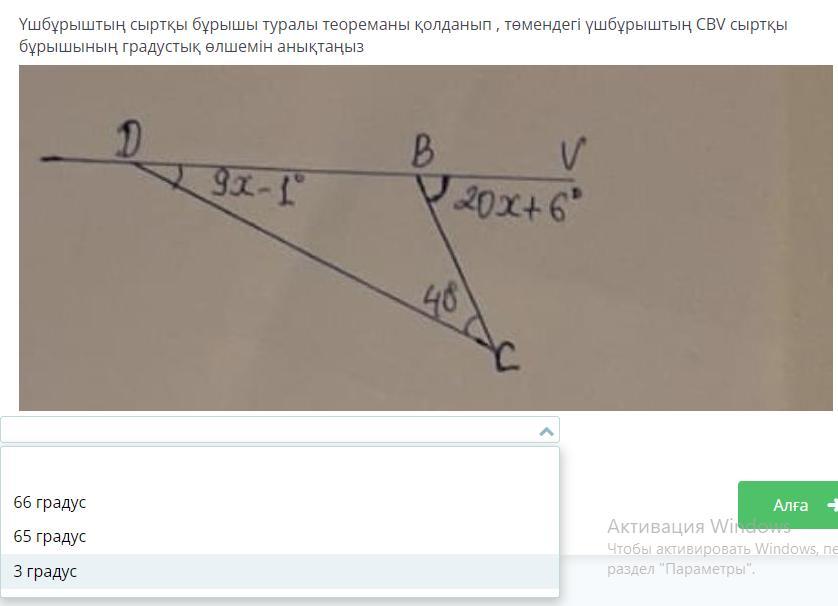
2Используя теорему о внешнем угле треугольника, определите степень в градусах внешнего угла CBV следующего треугольника.
Внешние углы двух разных углов треугольника равны друг другу. Периметр треугольника - 64 см, а одна из сторон - 6 см. Определите длины двух других сторон треугольника.
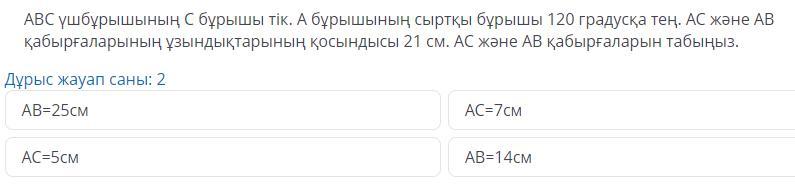
Угол c треугольника ABC прямой. Внешний угол угла A составляет 120 градусов. Сумма длин стен AC и AB составляет 21 см. Найдите стены AC и AB.


Ответы
Ответ:
Угол 125 градусов и угол 55 градусов называются односторонними и ВСЕГДА их сумма составляет 180 градусов
125+55=180 градусов
Если при пересечении двух прямых третьей секущей сумма односторонних углов равна 180 градусов,то прямые параллельны
Номер 2
Если внешние углы треугольника равны между собой,то равны и смежные им внутренние углы,а это обозначает,что треугольник равнобедренный,если одна из сторон равна 6 см,и это основание треугольника,а периметр равен 64 см,то каждая боковая сторона,а они в равнобедренном треугольнике равны между собой,равна
(64-6):2=29 сантиметров
Номер 3
Внешний и смежный ему внутренний угол в сумме равны 180 градусов
<А=180-120=60 градусов
Так как треугольник прямоугольный,то <В=180-(90+60)=30 градусов
Значит,АС+АВ=21 см ,где
АВ-гипотенуза
АС-катет,который расположен против угла 30 градусов
По определению,катет,лежащий против угла 30 градусов вдвое меньше гипотенузы
Катет-Х
Гипотенуза-2Х
Х+2Х=21
ЗХ=21
Х=21:3
Х=7
АС=7 см
АВ=7•2=14 см
Объяснение: