Question

Даю 30 баллов
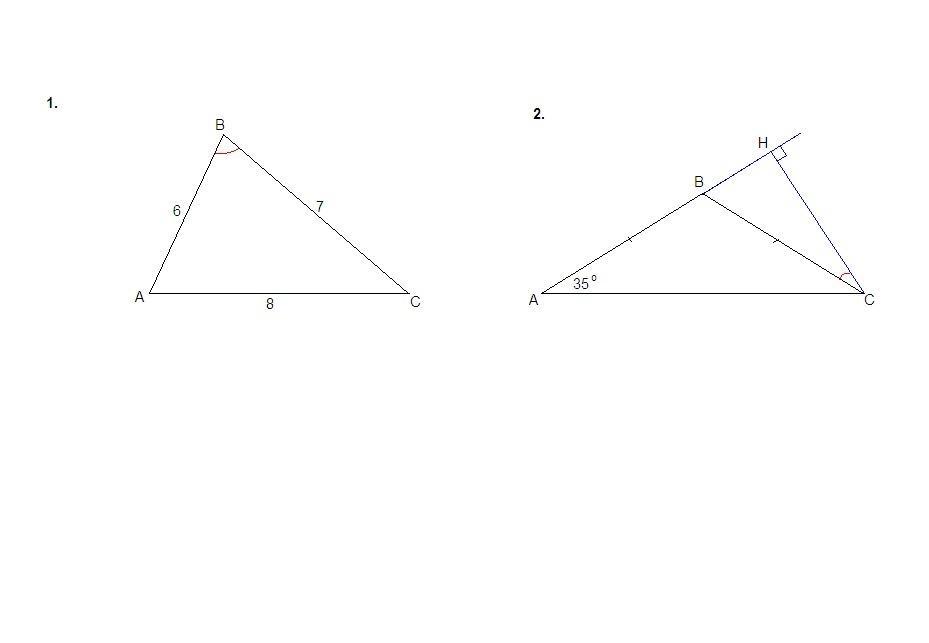
В треугольнике ABC известно, что AB = 6, BC = 8, cos ABC=7/8 Найдите AC.

Answer 1

Ответ:1.

По теореме косинусов:

АС² = АВ² + ВС² - 2·АВ·ВС·cos∠B

64 = 36 + 49 - 2·6·7·cos∠B

cos∠B = (36 + 49 - 64) / (2 · 6 · 7) = 21 / (2 · 6 · 7) = 1/4

Основное тригонометрическое тождество:

sin²∠B + cos²∠B = 1

sin∠B = √(1 - cos²∠B) = √(1 - 1/16) = √15/4

2.

СН - высота, проведенная к боковой стороне.

∠ВСН - искомый.

Углы при основании равнобедренного треугольника равны:

∠А = ∠С = 35°

∠НВС = ∠А + ∠С = 70°, так как внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

ΔНВС: ∠ВНС = 90°, ∠НВС = 70°, ⇒ ∠ВСН = 20°

Answer 2

Ответ:

4

Объяснение:

по теореме косинусов

AC^2=AB^2+BC^2-2AB*BC*cosabc

AC=✓(AB^2+BC^2-2AB*BC*cosabc)=✓(36+64-84)=✓16=4

вроде так