Предмет: Математика,
автор: Аноним
Помогите пожалуйста желательно с графиком даю 100 баллов
Приложения:
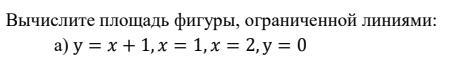
Ответы
Автор ответа:
1
Приложения:
Автор ответа:
0
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 89138841404
Предмет: Русский язык,
автор: 462196кирилл
Предмет: Русский язык,
автор: zoooooom
Предмет: Английский язык,
автор: Korasd
Предмет: Қазақ тiлi,
автор: мони20081906