Question

Теорема о сумме углов выпуклого n-угольника(доказательство)

Answer 1

Теорема: Сумма внутренних углов выпуклого n-угольника вычисляется по формуле: 180°(n - 2).

Доказательство:
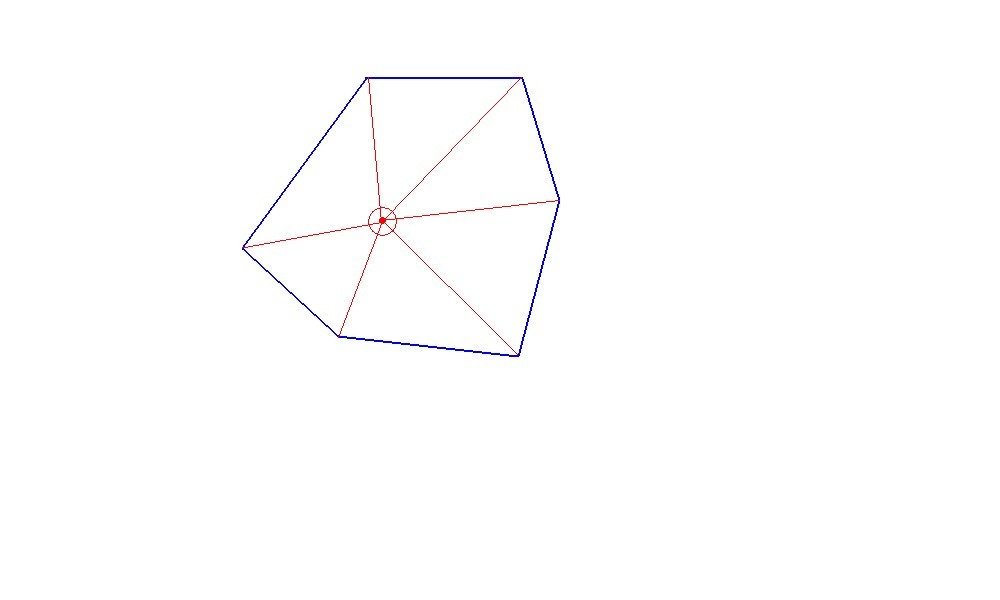
Отметим произвольную точку внутри выпуклого n-угольника и соединим ее с вершинами. Получим n треугольников.
Сумма углов одного треугольника равна 180°, значит сумма углов всех треугольников равна 180°n.
Но сумма углов всех треугольников включает в себя сумму внутренних углов выпуклого n-угольника и полный угол при вершине О, который надо отнять от получившейся суммы. Получим:
180°n - 360° = 180°(n - 2).
Доказано.