Предмет: Геометрия,
автор: vadim1despalov2008
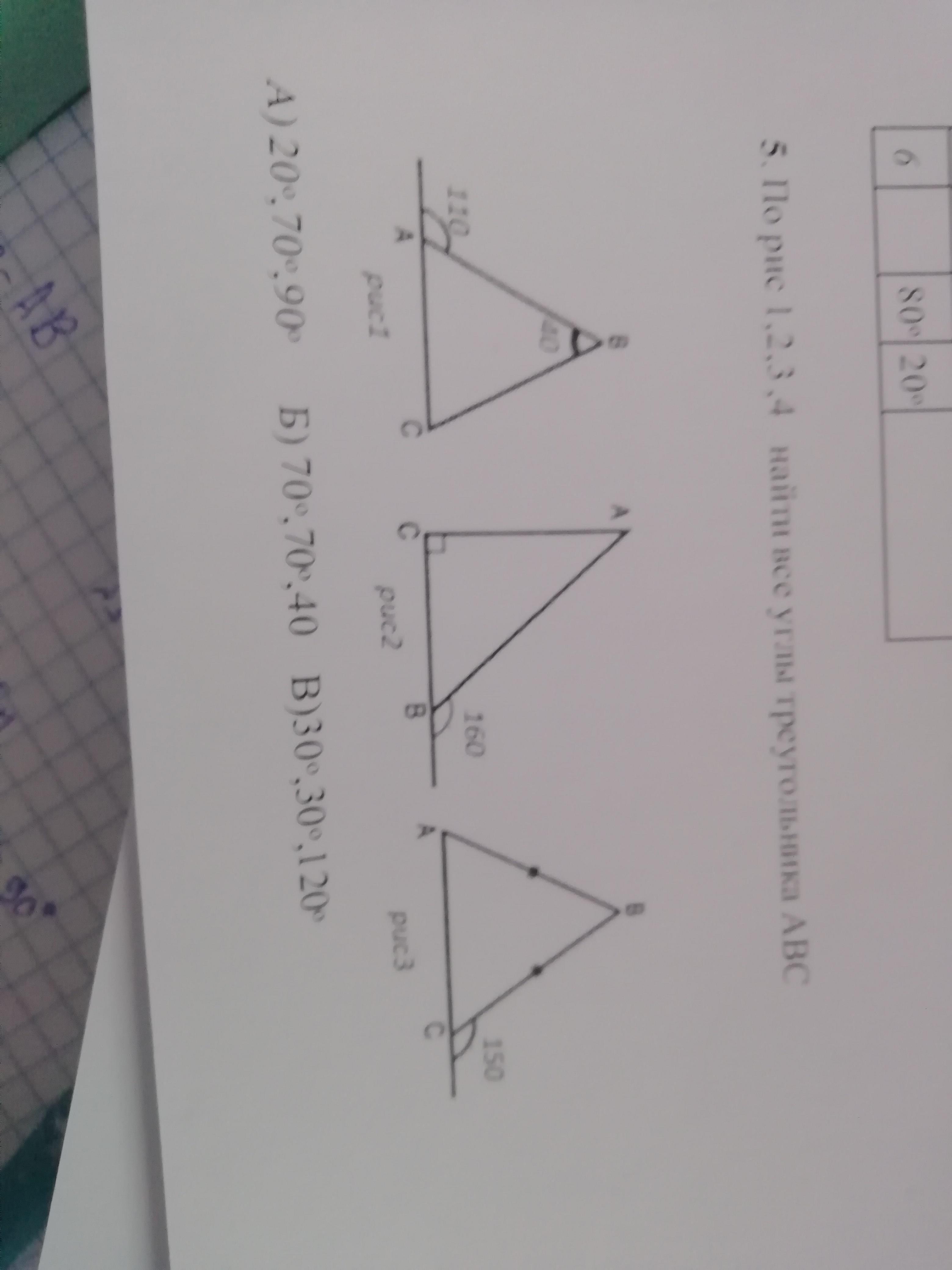
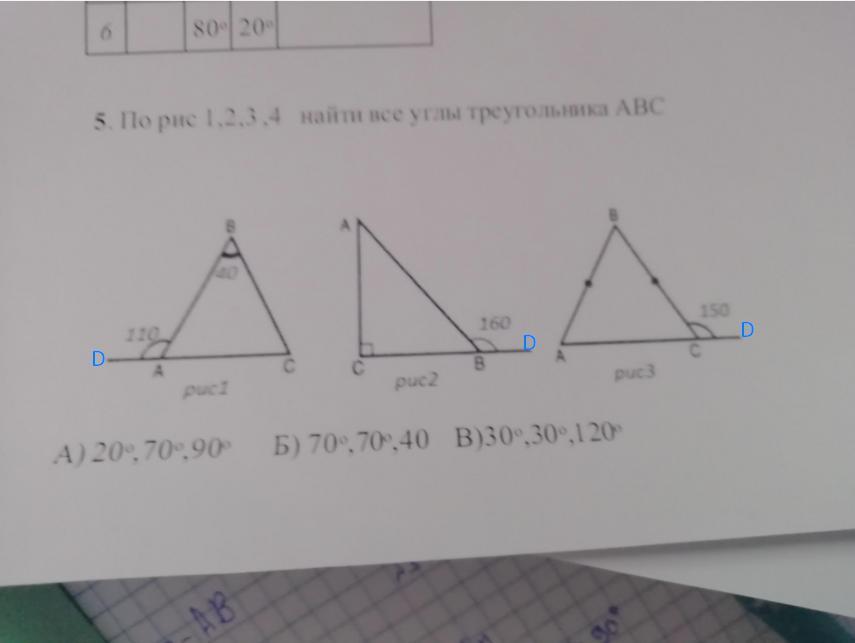
По рис 1 2 3 4 найти все углы треугольника ABC
Приложения:
Ответы
Автор ответа:
4
Ответ:
- рис. 1 - Б) 70°, 70°, 40°
- рис. 2 - А) 20°, 70°, 90°
- рис. 3 - В) 30°, 30°, 120°
Объяснение:
рис. 1
- Смежные углы в сумме дают 180°.
∠DAB и ∠BAC - смежные, тогда ∠DAB+∠BAC=180°, откуда ∠BAC=180°-∠DAB=180°-110°=70°.
- Сумма углов треугольника равна 180°.
∠BAC+∠ABC+∠BCA=180°, откуда ∠BCA=180°-∠BAC-∠ABC=180°-70°-40°=70°.
Итак, ∠BCA=70°, ∠BAC=70°, ∠ABC=40°.
рис. 2
- Смежные углы в сумме дают 180°.
∠DBA и ∠ABC - смежные, тогда ∠DBA+∠ABC=180°, откуда ∠ABC=180°-∠DBA=180°-160°=20°.
- Сумма острых углов прямоугольного треугольника равна 90°.
ΔACB - прямоугольный (∠ACB=90°), тогда ∠CAB+∠ABC=90°, откуда ∠CAB=90°-∠ABС=90°-20°=70°.
Итак, ∠ABC=20°, ∠CAB=70°, ∠ACB=90°.
рис. 3
- Смежные углы в сумме дают 180°.
∠BCA и ∠BCD - смежные, тогда ∠BCA+∠BCD=180°, откуда ∠BCA=180°-∠BCD=180°-150°=30°.
- В равнобедренном треугольнике углы при основании равны.
ΔABC - равнобедренный по условию, тогда ∠BAC=∠BCA=30°.
- Сумма углов треугольника равна 180°.
∠ABC+∠BCA+∠BAC=180°, откуда ∠ABC=180°-∠BCA-∠BAC=180°-30°-30°=120°.
Итак, ∠BCA=30°, ∠BAC=30°, ∠ABC=120°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: bika95
Предмет: Русский язык,
автор: kapitonovanikin
Предмет: Українська література,
автор: olyat20021
Предмет: Математика,
автор: znanija154
Предмет: Русский язык,
автор: Еленка163