Предмет: Геометрия,
автор: zibkim79
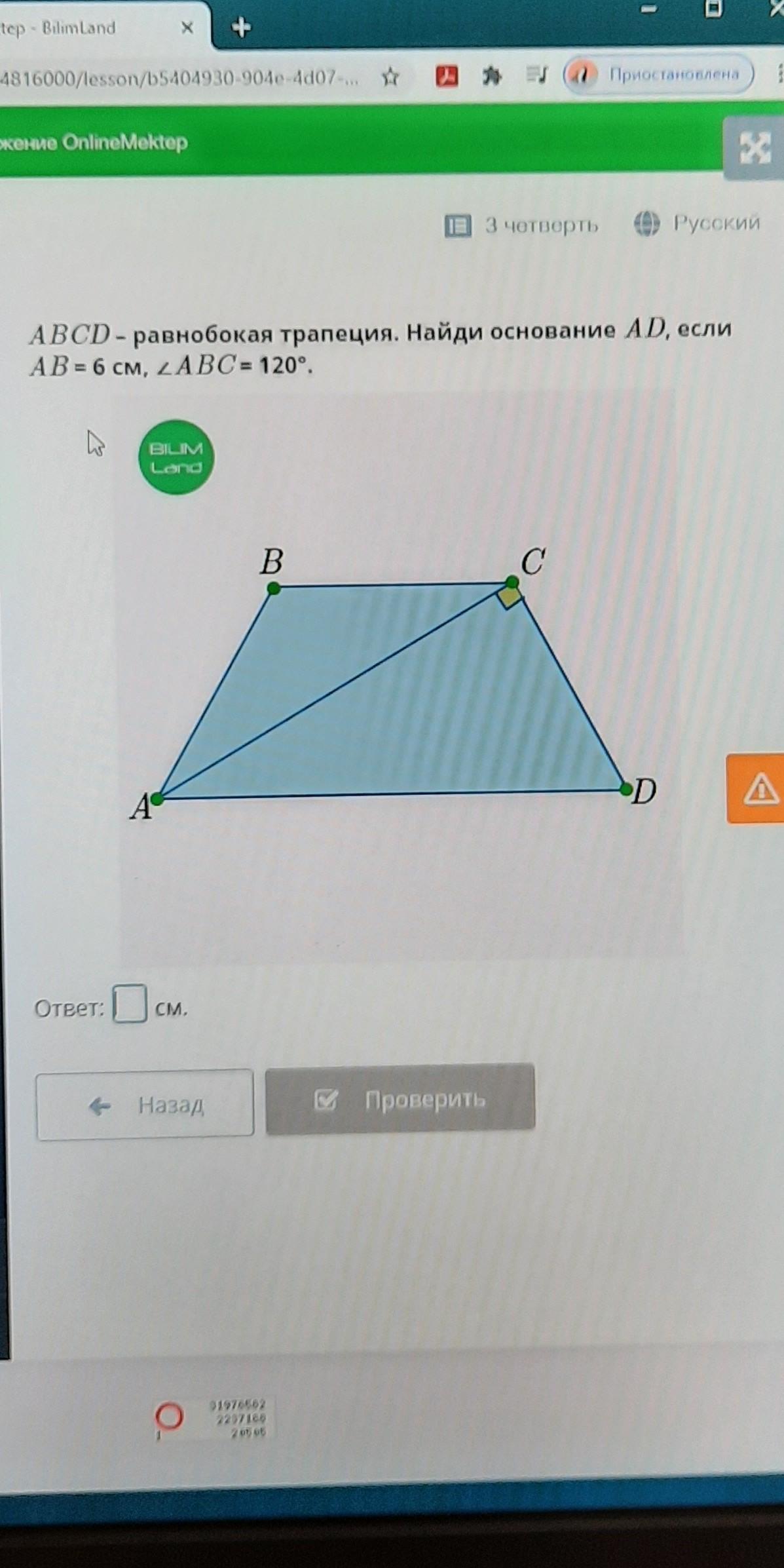
ABCD - равнобокая трапеция. Найди основание AD, если
AB = 6 см, ABC= 120°.
Приложения:
Ответы
Автор ответа:
0
Ответ: основание АD равно 12 см.
Объяснение:
Любая трапеция обладает таким свойством, что сумма углов, лежащих на одной боковой стороне, составляет 180°.
Значит, ∠BAD = 180 - ∠ABC = 180 - 120 = 60°.
Поскольку данная трапеция равнобокая, то ∠CDA = ∠BAD = 60° и CD = AB = 6 см.
Рассмотрим прямоугольный ΔACD:
CD — катет, прилежащий к ∠CDA, а AD — гипотенуза.
Выразим косинус ∠CDA:
.
Вычислим длину AD:
(см).
Похожие вопросы
Предмет: Русский язык,
автор: ромммм
Предмет: Русский язык,
автор: AlinaSol2001
Предмет: Русский язык,
автор: andrew1502200
Предмет: Русский язык,
автор: Mihailolom